This learning module covers:
Let us take an example. Assume Leo owns a share of GE, whose spot price today (S0) is $100. Rachel enters into a forward contract with Leo today to buy a share of GE at $110 after 1 year.
The terms, parties, and ways to settle the contract are described below:
The above example is shown in a generic way in the diagram below. It shows the transactions from a buyer’s perspective at times t = 0 when the contract is initiated and time t = T, when the contract expires.

Interpreting the notation and key features of a forward contract:
The forward price agreed at the initiation date of the contract is the spot rate compounded at the risk-free rate over the life of the contract.
F0 (T)= S0 x (1 + r)T
Assuming a risk-free rate of 10%, spot price of S0= $100, and time period of 1 year, we calculate the forward price as:
F0 (T)= S0 x (1 + r)T= 100 × (1.1)1 = 110
Why is the forward price equal to the spot rate compounded at the risk-free rate over the contract period?
In theory, if Rachel did not enter into the forward contract, then she could invest $100 for period T in a risk-free asset and earn 10% or $110 after 1 year. So, the forward contract must earn the risk-free rate as an excess return will result in an arbitrage opportunity.
Value of a forward contract at initiation
Value of a forward contract at initiation = 0
The value of a forward contract at initiation is zero because neither party pays any money to the other. There is no value to either party.
Value at expiration for the long party:
Vt (T) = ST– F0 (T)
where:
ST = spot price of the underlying
F0 (T) = forward price agreed in the contract
The value of a forward contract is positive to the long party if ST > F0 (T) and negative if ST < F0 (T) at expiration.
Value at expiration for the short party:
Vt (T)= – (ST– F0 (T))
The value of a forward contract is positive to the short party if F0 (T)>ST and negative if F0 (T)<ST at expiration.
If the spot price at time T is 115, then Rachel (long) gets the asset by paying 110 and can immediately sell it for 115 at the then market price. Value to the long = ST– F = 115 – 110 = 5.
Value of a forward contract during the life of the contract
Value during the life of the contract Vt = St – F/(1 + r)(T-t)
This is the difference between the spot price at time t, and the present value of forward price for the remaining life of the contract. In our example, after 6 months at t = 0.5, if St = 116, then Vt = 116 – 110/(1.1)(1-0.5) = 11.12. Since the price has gone up, the value to the long party is positive.
Instructor’s Note
As market conditions change, only the value of a forward contract changes. Its price does not change as it is fixed at contract initiation.
Thus, the passage of time and spot price changes causes the MTM value of a forward contract to fluctuate representing a gain or loss to contract participants. Exhibit 5 from the curriculum shows this relationship, assuming a constant risk-free rate over the life of a contract for long and short forward contract positions.

Pricing and Valuation of Forward Contracts with Additional Costs or Benefits
Now, let us consider an asset with benefits or income(I) and costs (C). How is the forward price for such an asset calculated? The forward price of an asset with benefits and/or costs is the spot price compounded at the risk-free rate over the life of the contract minus the future value of those benefits and costs.
F0 (T)= (S0 – PV0 (I)+PV0 (C) ) x (1 + r)T
where:
PV0 (I) = present value of the benefit. It is subtracted from the spot price because if you own the asset, you receive any benefits associated with the asset, during the life of the contract.
PV0 (C) = present value of costs incurred on the asset during the life of the contract. These costs make it more expensive to hold the asset and hence increase the forward price.
In the previous example, assume $10 is the present value of benefits from the asset and $20 is the present value of costs associated with holding the asset. The forward price at time 0 when Rachel enters into the contract is:
F0 (T) = (100 – 10 + 20) (1.1)1 = 121
Value of the forward contract
At any time t over the life of the contract, the MTM value of the forward contract, Vt(T), will depend on the difference between the current spot price adjusted for any remaining costs or benefits from time t through maturity.
Vt (T)=(St – PVt (I)+PVt (C))-(F0 (T))/(1+r)(T-t)
Example: Equity Forward Valuation
(This is based on Example 4 from the curriculum.)
A company agrees to deliver 1,000 Unilever (UL) shares to a financial intermediary in six months under a forward contract at a price of EUR 50.6311 per share. Unilever pays a quarterly dividend of EUR 0.30 three months after contract inception and at time T, and the risk-free rate (r) is 5%. Calculate the forward contract breakeven price, St, where Vt(T) = MTM = 0 four months after contract inception if the risk-free rate, r, remains unchanged at 5%.
Solution:
Calculate the present value of the dividend per share, PVt(I), given that the second dividend will be paid in two months:
PVt(I) = EUR0.30(1.05) – 2/12 = EUR0.2976
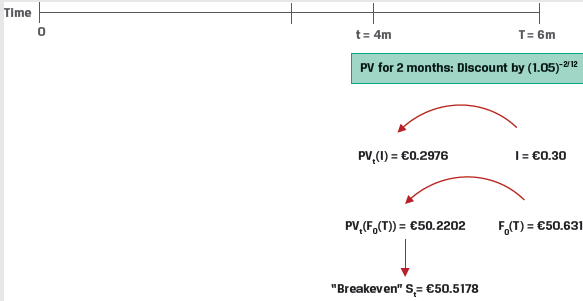
With PVt(C) = 0, solve for Vt(T) = 0 four months after contract inception,
Vt (T)=(St – PVt (I)+PVt (C))-(F0 (T))/(1+r)(T-t)
0 = (St − 0.2976) − 50.6311(1.05)-2/12
St = EUR50.2202 + EUR0.2976
= EUR50.5178
Hightest Capital’s breakeven spot rate, St (i.e., where Vt(T) = 0), four months after inception of the forward contract is therefore EUR50.5178 per share.
Pricing and Valuation of Foreign Exchange Forwards
The forward price for a FX forward contract is calculated as:
F0 (T)=S0 e((r_f-r_d)T)
At any given time t, the MTM value of the FX forward is the difference between the current spot FX price (St) and the present value of the forward price discounted by the current difference in risk-free rates (rf − rd) for the remaining period through maturity,
Vt (T) = St– (F0 (T))/e((r_f-r_d)(T-t))
Example: FX Forward MTM
(This is based on Example 5 from the curriculum.)
A company has entered into a long one-year USD/EUR forward contract. It has agreed to purchase EUR1,000,000 in exchange for USD1,201,000 in one year. At time t=0, when the contract is initiated, the USD/EUR spot exchange rate is 1.192 , the one-year USD risk-free rate is 0.50%, and the one-year EUR risk-free rate is −0.25%.
Describe the MTM impact on the FX forward contract from the company’s perspective if the one-year USD risk-free rate instantaneously rises by 0.25% once the contract is initiated, with other details unchanged.
Solution:
The MTM value at t=0 can be calculated as:
Vt (T) = S0– (F0 (T))/e((r_f-r_d)(T))
S0 = 1.192
F0 = 1,201,000/ 1,000,000 = 1.201
rf = 0.75%
rd = -0.25%
T = 1
Using these inputs,
Vt (T)= (1.192-1.201)/e(0.0075+0.0025) =0.00295 USD/EUR
Yield to Maturity (YTM)
The YTM is the discount rate that, when applied to a bond’s promised cash flows, equates those cash flows to the bond’s market price.
Suppose we are provided the following data for three recently issued annual fixed-coupon government bonds:
| Years to Maturity | Annual Coupon | PV (per 100 FV) |
| 1 | 1.50% | 99.125 |
| 2 | 2.50% | 98.275 |
| 3 | 3.25% | 98.00 |
Using this information we can calculate the YTM for each bond as follows:
Bond 1: N = 1, PV = -99.125, PMT = 1.50, FV = 100 → CPT I/Y = 2.3960%
Bond 2: N = 2, PV = -98.275, PMT = 2.50, FV = 100 → CPT I/Y = 3.4068%
Bond 3: N = 3, PV = -98.00, PMT = 3.25, FV = 100 → CPT I/Y = 3.9703%
Zero Rates
A zero rate (also called spot rate) is the YTM on zero-coupon bonds. They are denoted as (z1, z2, ….zN), where zi is the zero rate for period i.
Zero rates can be computed from the YTM of coupon paying government bonds through a process called ‘bootstrapping’.
Continuing with our example, lets add a YTM column to our data on the 3 coupon paying government bonds.
| Years to Maturity | Annual Coupon | PV (per 100 FV) | YTM |
| 1 | 1.50% | 99.125 | 2.3960% |
| 2 | 2.50% | 98.275 | 3.4068% |
| 3 | 3.25% | 98.00 | 3.9703% |
Starting with the one-year bond, which consists of a single cash flow at maturity, we can solve for the one-year zero rate (z1) as follows:
One year:
99.125=101.5/(1+z1)1 ;z1=2.3960%
Instructor’s Note: Since the 1-year bond consists of a single cash flow at maturity, the zero rate and the YTM are identical.
Since all cash flows at time t = 1 are discounted at z1, we can substitute z1 into the two-year fixed-coupon bond calculation to solve for the zero-coupon rate at the end of the second period (z2):
Two year:
98.275=(2.5/91.02396) + (102.50/(1+z2))2 ;z2=3.4197%
We then substitute both z1 and z2 into the three-year bond equation to solve for the zero-coupon cash flow at the end of year three (z3):
Three year:
98.00 = 3.25/(1.02396) + [3.25/(1.034197)2] + (103.25/(1+z3)3 ;z3=4.0005%
Discount Factors
The price or present value of a risk-free single-unit payment (e.g., $1, €1, or £1) after N periods is called the discount factor, denoted by DFN.
Discount factors can be calculated from zero rates using the formula:
DFi=1/[1+Zi]i
Continuing with our example, the discount factors for years 1,2, and 3 can be computed as:
One-year: DF1 = 1/(1 + z1); DF1 = 0.976601
Two-year: DF2 = 1/(1 + z2)2; DF2 = 0.934961
Three-year: DF3 = 1/(1 + z3)3; DF3 = 0.888982
A discount factor can also be interpreted as the price of a zero-coupon bond.
Forward Rates
A forward rate is the interest rate that is determined today for a loan that will be initiated at a future time period. FA,B represents a forward rate for a loan initiated A years from today with further maturity of B years. For example, F2,3 represents the forward rate for a loan which starts at the end of year 2 and matured at the end of year 5.
Given a set of zero rates we can calculate the ‘implied forward rates’. Continuing with our example, let us present the zero rates we calculated in a table.
| Years to Maturity | Zero Rate |
| 1 | 2.3960% |
| 2 | 3.4197% |
| 3 | 4.0005% |
Over a two-year period an investor faces the following investment choices:
Based on the no-arbitrage principal both options should give the same results. Therefore,
USD100 × (1 + z1) × (1 + IFR1,1) = USD100 × (1 + z2)2
USD100 × (1.02396) × (1 + IFR1,1) = USD100 × (1.034197)2
IFR1,1 = 4.4536%
This is illustrated in the figure below.
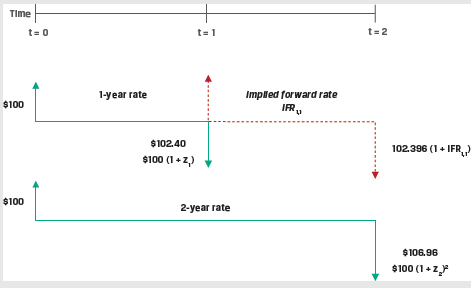
A general formula for the relationship between two spot rates (zA, zB) and the implied forward rate (IFRA,B–A):
(1 + zA)A × (1 + IFRA,B–A)B–A = (1 + zB)B
Using this formula, we can solve for the one-period rate in two periods (IFR2,1) as follows:
(1 + z2)2 × (1 + IFR2,1)1 = (1 + z3)3
(1.034197)2 × (1 + IFR2,1) = (1.040005)3
IFR2,1 = 5.1719%
Forward Rate Agreements (FRAs)
A forward rate agreement (FRA) is an OTC derivatives contract in which counterparties agree to apply a specific interest rate to a future period. FRAs allow us to lock in a rate today for a loan in the future and act as a hedge against interest rate risk.
The FRA buyer, or long position, agrees to pay an interest based on a fixed rate and receive interest based on a future market reference rate. The interest payments are calculated on a hypothetical notional amount.
Exhibit 9 from the curriculum shows the FRA mechanics at t = 0 and settlement at time A.
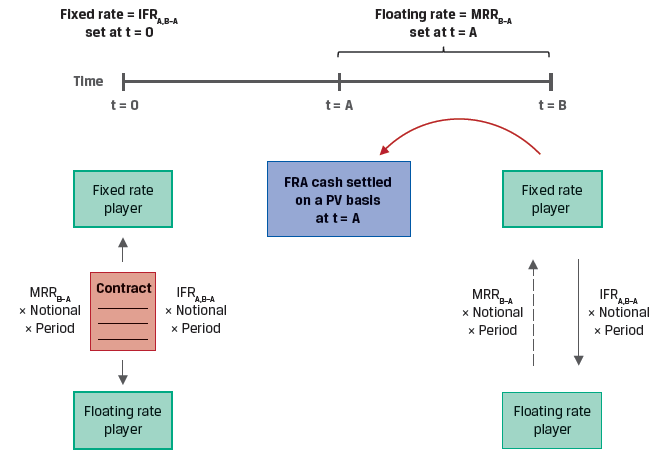
The payoffs on an FRA are determined by market interest rates at expiration:
Example: FRA
(This is Example 5 from Knowledge check)
A counterparty agrees to be the FRA fixed-rate receiver on a one-month AUD MRR in three months’ time based on a AUD150,000,000 notional amount. If IFR3m,1m at contract inception is 0.50% and one-month AUD MRR sets at 0.35% for settlement of the contract, calculate the settlement amount and interpret the results.
Solution:
A short FRA position, or fixed-rate receiver, agrees to pay interest based on a market reference rate determined at settlement and receives interest based on a pre-agreed fixed rate, the implied forward rate (IFR3m,1m). Since AUD MRRB-A at settlement is below the pre-agreed fixed rate, the FRA fixed-rate receiver realizes a gain and receives a net payment based on the following calculation:
Net Payment = (IFRA,B-A − MRRB-A) × Notional Principal × Period
= (0.50% − 0.35%) × AUD150,000,000 × (1/12)
= AUD18,750 at the end of the period
Solve for the present value of settlement given the contract is settled at the beginning of the period, using MRRB-A as the discount rate:
Cash Settlement (PV) = AUD18,750.00/(1 + 0.35%/12)
= AUD18,744.53