LM09 Option Replication Using Put–Call Parity

Part 1

1. Introduction

This learning module covers:

• Put-call parity for European options
• Put-call forward parity for European options
• Put-call parity application to explain firm value

2. Put–Call Parity

The four instruments in a put-call parity are as follows:

• Asset: An asset such as a stock with no carrying costs and no interim cash flows. At time 0, the price of the stock is S
• Zero-coupon bond: A zero-coupon bond with a face value of X that matures at time T. At time 0, the value of this bond is
• Call option: A call option on the stock with a strike price of X that expires at time T. S_T is the underlying price at expiration T.
• Put option: A put option on the stock with a strike price of X that expires at time T.

Note: The strike price, X, of the options is the same as the par value of the bond.

According to put-call parity, fiduciary call = protective put.

Protective Put:

A protective put is to buy the underlying and buy a put option on it. The cost of this strategy is:

p₀+S₀

A protective put is like buying insurance for an asset you own, specifically a stock, to protect against a downside. For instance, you own 1,000 shares of Apple, the market is highly volatile and you are worried about a huge decline in the near term. To limit the downside risk, you can buy a put option on the stock by paying a premium. This is called a protective put.

Interpretation:

• As you can see, the downside risk is limited to the premium paid for the put. If the underlying price falls below X, it can be still be sold at X by exercising the put option.
• If the underlying rises above X, then it can be sold at the market price and the put option expires worthless.

Fiduciary Call:

A fiduciary call is a long call plus a risk-free bond. The cost of this strategy is:

c₀+

The diagram below shows the payoff for a fiduciary call:

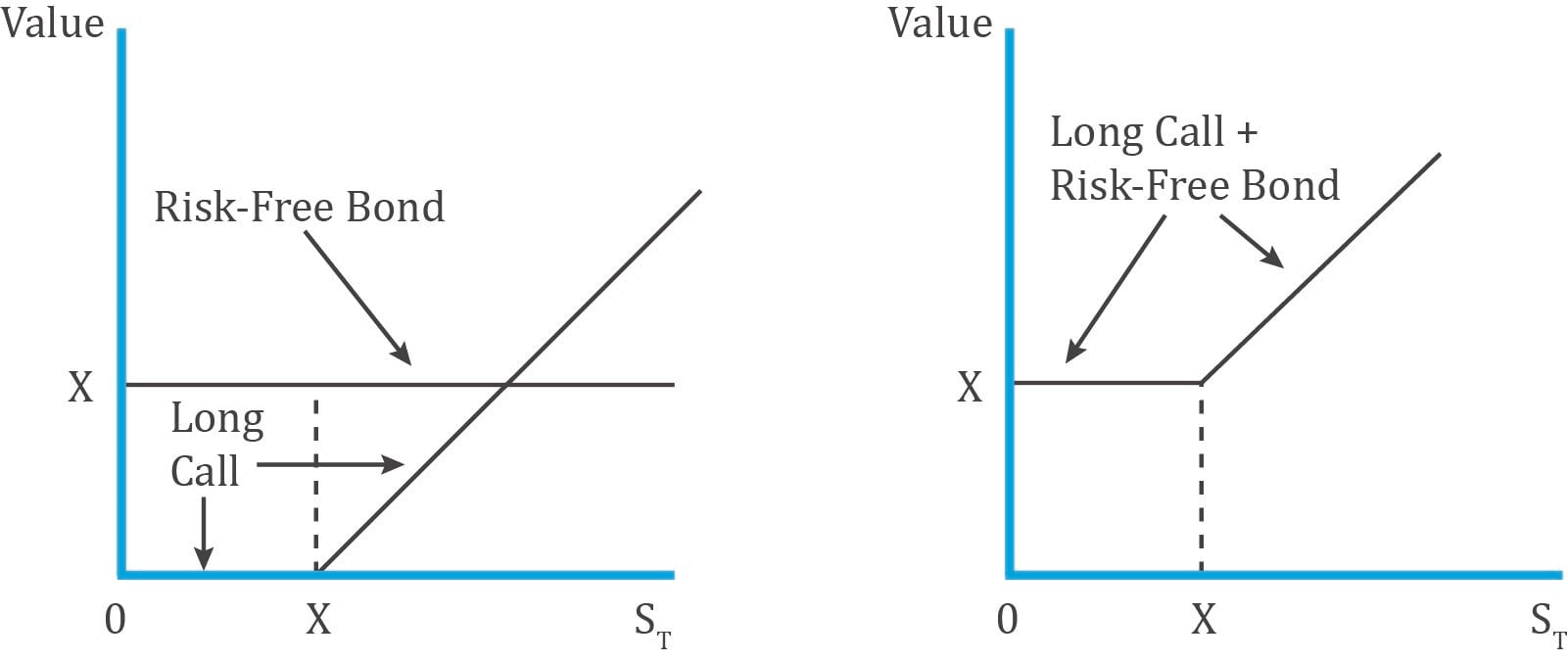
Therefore, according to put-call parity:

c₀ +   = p₀ + S₀

In other words, under put–call parity, at t = 0 the price of the long call plus the risk-free asset must equal the price of the long underlying asset plus the long put.

The table below shows how the fiduciary call is equal to the protective put under two possible scenarios: when the stock is above the exercise price (call is in the money) and the stock is below the exercise price (put is in the money).

Outcome at time T when: &#8594;	Put expires in the money (ST < X)		Call expires in the money (ST > = X)
Protective put
Asset	ST		ST
Long puts	X-ST		0
Total	X		ST
Fiduciary call
Long call	0		ST – X
Risk-free bond	X		X
Total	X		ST
		Fiduciary Call		Protective Put
Constituents		Long call + risk-free bond		Long put + stock
Equation		c0+		p0+S0
Payoff at T if call expires in the money (ST > = X)		ST		ST
Payoff at T if put expires in the money (ST < X)		X		X

If, at time 0, the fiduciary call is not priced the same as the protective put, then there is an arbitrage opportunity.

Example: Put-Call Parity

(This is based on Example 1 from the curriculum.)

A stock currently trades at INR295 per share. An investor is considering the purchase of a six-month put on this stock at an exercise price of INR265. A six-month call option with the same exercise price trades in the market at INR59. What should the investor expect to pay for the put if the relevant risk-free rate is 4%?

Solution:

According to put call parity:

c₀+ = p₀ + S₀

59 + = p₀ + 295

59 + 259.85 = p₀ + 295

p₀ = INR23.85

The investor should expect to pay a six-month put option premium of p₀ = INR23.85

3. Option Strategies Based on Put–Call Parity

The put-call parity relationship can be rearranged in the following ways:

Synthetic call:

Synthetic bond:

Synthetic stock: S₀ = c₀+  – p₀

Synthetic put: p₀ = c₀+  – S₀

These equations allow us to replicate an instrument by using the other three instruments. For example, a put option can be replicated by a combination of a long call, a long risk-free bond and a short position in the underlying.

We can also compare the price of an actual instrument to its synthetic version. If the two prices are different, we can generate riskless profits by exploiting the mispricing.

4. Put–Call Forward Parity and Option Applications

In earlier readings we saw that:

Long asset + Short forward = Long risk-free bond

i.e. Asset – Forward = Risk-free Bond

(Long positions are shown as +ve and short positions as -ve)

Rearranging, we get:

Asset = Forward + Risk-free bond

We will use this relationship to come up with the put-call forward parity.

5. Put–Call Forward Parity

Protective put: Asset + Put

If we substitute the ‘asset’ part in a protective put with a forward and risk-free bond we get:

Synthetic protective put = Forward + Risk-free bond + Put

Here, the risk-free bond has a par value equal to the forward price of F₀ (T).

The cost this synthetic protective put is:

+p₀

The cost of entering a forward contract at t=0 is zero as it requires no upfront payment.

The risk-free bond with par value F₀ (T) can be purchased at t=0 for

The put option premium at t=0 is p₀

The table below shows that the payoff for a protective put with an asset and a synthetic protective put with a forward contract is the same when the put expires in and out of the money.

Interpretation:

• Value of the forward contract at expiration = S_T – F₀ (T).
• Notice that the value of the forward contract at expiration is the same irrespective of whether the put expires in or out of the money.

The put-call parity relationship can now be written as:

Synthetic protective put = Fiduciary call

Long Put + Long forward + Risk-free bond = Bond + Call

The table below shows that the payoffs for fiduciary call is equal to synthetic protective put when call and put expire in the money.

6. Option Put–Call Parity Applications: Firm Value

The put-call parity relationship can also be used to model the value of a firm to equity and debt holders.

Assume that at time t = 0, a firm with a market value of V₀ has access to borrowed capital in the form of zero-coupon debt with a face value of D. The value of equity at t = 0 is E₀.

The firm value can be expressed as:

V₀ = E₀ + PV(D)

When the debt matures at T, there are two possible outcomes:

1. Solvency (V_T > D): The firm value exceeds the face value of debt and we say that the firm is solvent. In this case:
   • Debtholders are paid in full and receive D.
   • Shareholders receive the residual: E_T = V_T – D.
2. Insolvency (V_T < D): The firm value is below the face value of debt and we say that the firm is insolvent. In this case:

• Debtholders have a priority claim on assets and receive V_T (which is less than D).
• Shareholders don’t receive any funds, E_T =0.

Thus,

Shareholder payoff is max(0, V_T – D) and

Debtholder payoff is min(V_T, D).

These payoff profiles can be expressed in terms of options:

• Shareholders hold a long position in the underlying firm’s assets (V_T) and have purchased a put option on firm value (V_T) with an exercise price of D; that is, max(0, D – V_T).

Or we can also say that shareholders have purchased a call option on the firm’s assets with an exercise price of D.

• Debtholders hold a long position in a risk-free bond (D) and have sold a put option to shareholders on firm value (V_T) with an exercise price of D.

Exhibit 9 from the curriculum shows the payoff profiles for shareholders and debtholders.

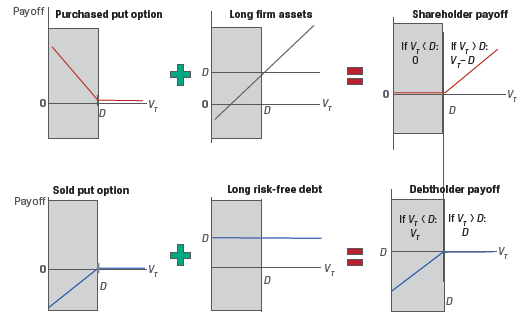
Revisiting the put-call parity relationship:

S₀ + p₀ = c₀ + PV(X)

Replacing ‘S₀’ with ‘V₀’ and ‘X’ with ‘D’ we get:

V₀ + p₀ = c₀ + PV(D)

V₀ = c₀ + PV(D) – p₀

Thus, the value of the firm is the value to the shareholders (represented by the call option c₀) plus the value to debt holders (represented by the risk-free debt and a sold put option p₀).

Share on :