IFT Notes for Level I CFA^® Program

LM02 Forward Commitment and Contingent Claim Features and Instruments

Part 1

1. Introduction

A derivative is a financial instrument that derives its value from the performance of an underlying.

This learning module covers the basic features and valuation of the following derivative instruments:

Firm commitments: Forwards, futures, and swaps
Contingent claims: Options and credit derivatives

2. Forwards

A firm commitment is a contract that requires both the long and short parties to engage in a transaction at a later point in time (the expiration) on terms agreed upon today. The parties establish the identity and quantity of the underlying, the manner in which the contract will be executed or settled when it expires, and the fixed price at which the underlying will be exchanged. Both the parties – the buyer and the seller – have an obligation to engage in the transaction at a future date in a firm commitment.

We will look at the three types of firm commitments: forward contracts, futures contracts, and swaps.

Forward Contracts

A forward contract is an over-the-counter derivative contract in which two parties agree to exchange a specific quantity of an underlying asset at a later date at a fixed price they agree on when the contract is signed. It is a customized and private contract between two parties.

Terms of a forward contract

Where the asset will be delivered.
Identity of the underlying.
Number of units or quantity of the underlying. For example, if the underlying is gold and the price is fixed per gram, the number of grams to be delivered must be specified.
It is a customized contract between two parties and not traded over the exchange.

Risk of a forward contract

The long hopes the underlying will increase in value while the short hopes the asset will decrease in value. One of the two will happen and whoever owes money may default.
With forward contracts, no money is exchanged at the start of the contract. Further, the value of the contract is zero at initiation.

Payoff for long and short:

The diagram below illustrates the payoff diagram for long and short in a forward contract:

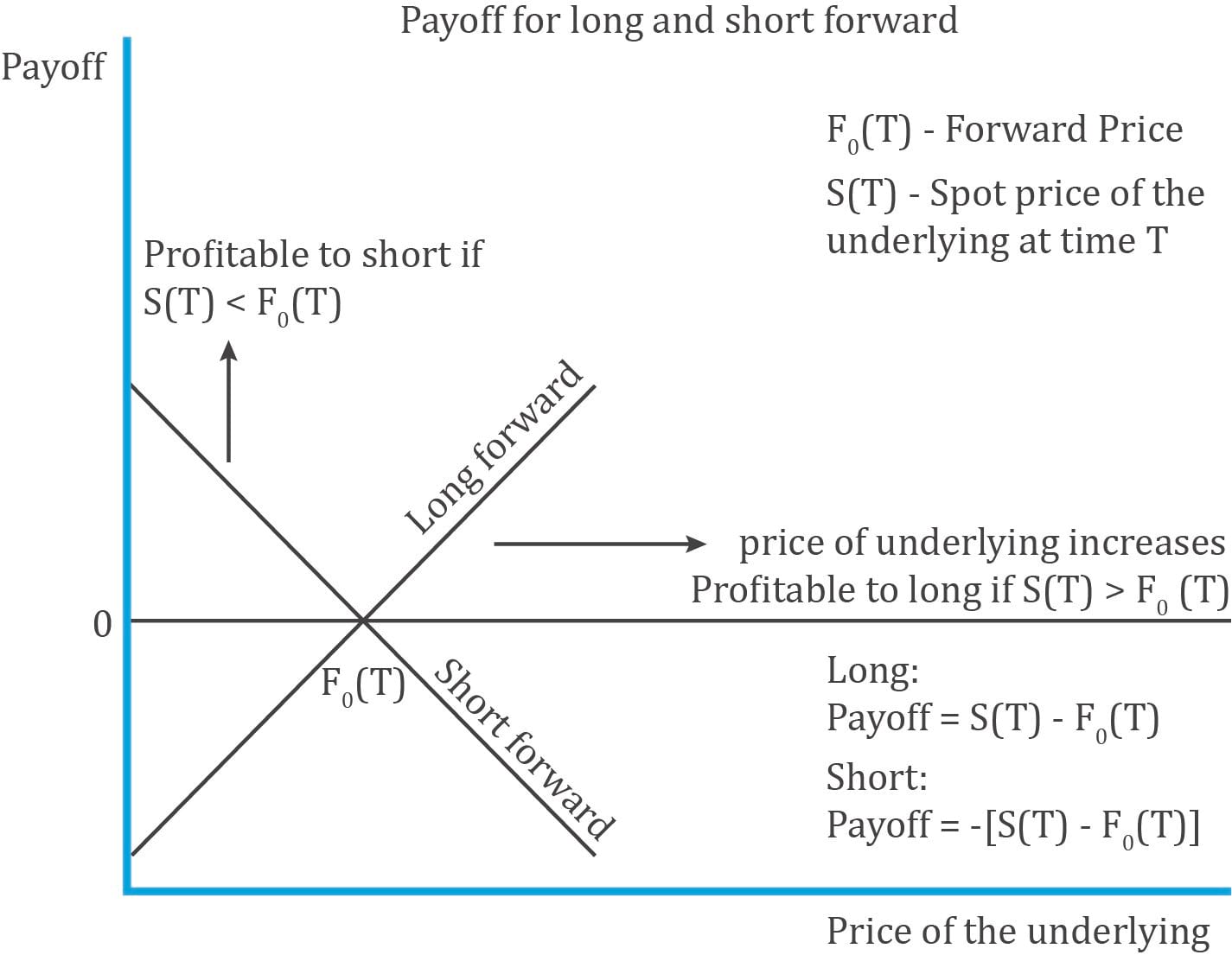
Notation:

= price of the underlying at time 0; = price of the underlying at time T
= forward price fixed at inception at time t = 0
T = when the forward contract expires

The long party benefits if the spot price increases and goes above the forward price. The short party benefits if the spot price decreases and goes below the forward price.

Example

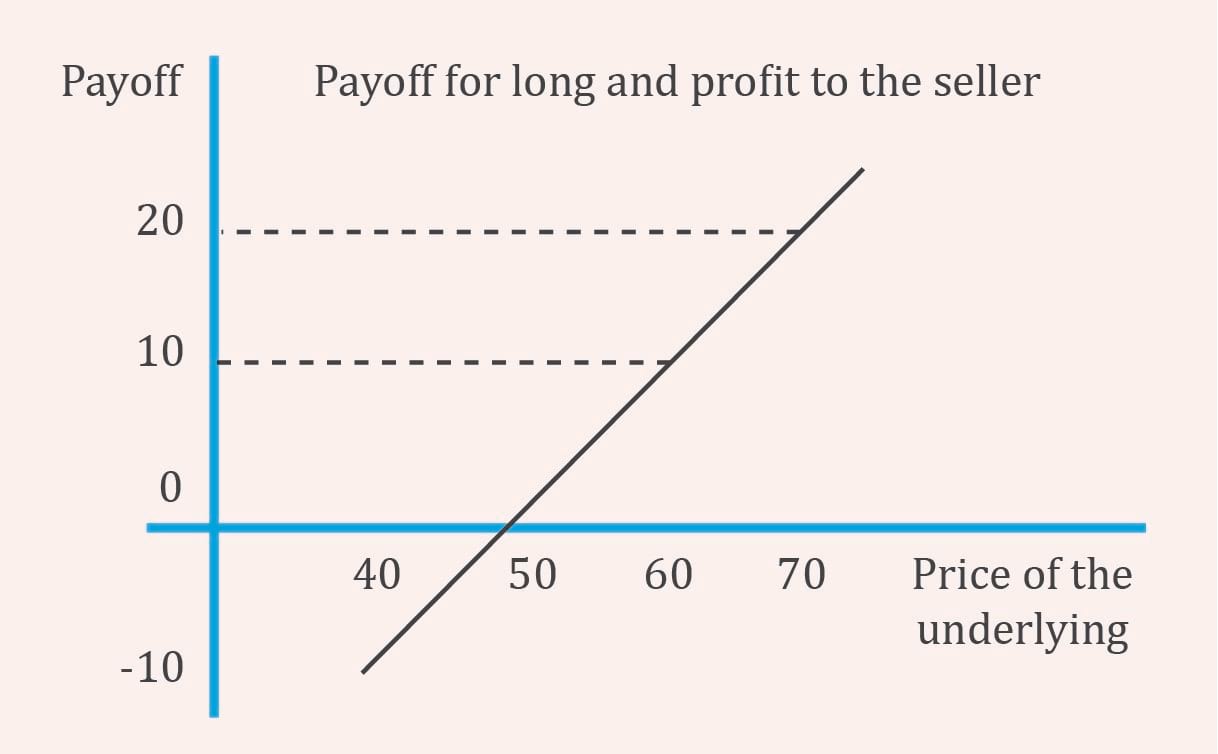
Whizz wants to sell 500 shares of beverage maker FTC to Fizz at $50 per share after 180 days. What happens if the market price of FTC at expiry is $50, $60, $70 or $40?

Solution:

Fizz is the long party and Whizz is the short party.

At expiry from Fizz’s perspective (long) when market price is:

$50: payoff is 0 and no one gains or loses

$60: long gains by $10

$70: long gains by $20

$40: long loses by $10 as he can buy the asset cheaper by $10 directly from the market instead of paying $50 to Whizz

From Whizz’s perspective, it is exactly the opposite to that of Fizz. When the share price increases to $70, he loses $20 as he can sell it in market for $70 but is selling for only $50 to Fizz.

The payoff for the long is depicted diagrammatically below:

3. Futures

A futures contract is a standardized derivative contract created and traded on a futures exchange such as the Chicago Mercantile Exchange (CME). In a futures contract, two parties agree to exchange a specific quantity of the underlying asset at an agreed-upon price at a later date. The buyer agrees to purchase the underlying asset from the other party, the seller. The agreed-upon price is called the futures price.

There are some similarities with a forward contract: two parties agreeing on a contract, an underlying asset, a fixed price called the futures price, a future expiry date, etc. But the following characteristics differentiate futures from a forward:

The contracts are standardized.
They are traded on a futures exchange.
The fixed price is called futures price and is denoted by (Forward prices are usually represented by F.)
The biggest difference is that gains or losses are settled on a daily basis by the exchange through its clearinghouse. This process is called mark to market(MTM).
Settlement price is the average of final futures trades and is determined by the clearinghouse.
The futures price converges to a spot price at expiration.
At expiry: the short delivers the asset and the long pays the spot price.

Let us take an example. Assume Ann enters into a contract to buy 100 grams of gold at $55 per gram after 90 days. The futures price is $55. At the end of day 1, the futures price is $58. There is a gain of $3. So, $300 ($3 per gram x 100 grams) is credited to Ann’s account. This is called marking to market. The account maintained by Ann is called the margin account.

Initial margin is the amount that must be deposited in a futures account before a trade is made. Associated with the initial margin is another figure called the maintenance margin which is the amount of money each participant must maintain in their accounts after the trade is initiated. If the margin balance falls below the maintenance margin additional funds must be deposited to bring the balance up to the initial margin amount.

To limit the potential losses from counterparty default, some futures contracts may limit daily price changes. These price limits set a band relative to the previous day’s settlement price within which all trades must take place. If price reaches the band limit, trading stops until two parties agree on a trade at a price within the prescribed range. In some cases, exchanges may use a circuit breaker – which pause intraday trading for a brief period, if a price limit is reached.

4. Swaps

A swap is a firm commitment between two counterparties to exchange a series of cash flows in the future. Typically, one cash flow stream is variable based on a market reference rate that resets each period; and the other cash flow stream is fixed or may vary based on a different underlying asset or rate.

Interest rate swaps are the most common type of swaps. Here, a fixed exchange rate is exchanged for a floating interest rate. The counterparty paying variable cash flows is called the floating rate payer; and the counterparty paying fixed cash flows is called the fixed rate payer. This is illustrated in Exhibit 3 of the curriculum.

The market reference rate (MRR) paid by the floating-rate payer resets every period, while the fixed rate (also called the swap rate) remains constant, as shown in Exhibit 4.

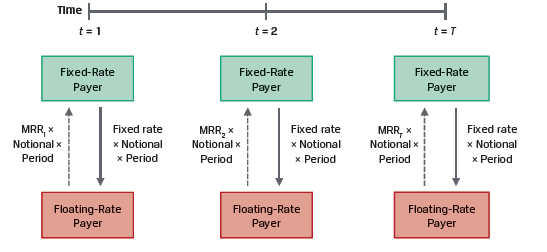
The payments are based on an agreed upon notional principal. The notional principal is usually not exchanged, but only used to calculate the payments. The payments are typically netted. A fixed rate payer receives a net payment if the MRR exceeds the fixed rate for a given period. Swaps allow investment managers to change portfolio duration without trading bonds.

Example: Fyleton Investments Swap

(This is Example 4 from the curriculum.)

Fyleton Investments has entered a five-year, receive-fixed GBP200 million interest rate swap with a financial intermediary to increase the duration of its fixed-income portfolio. Under terms of the swap, Fyleton has agreed to receive a semiannual GBP fixed rate of 2.25% and pay six-month MRR.

Calculate the first swap cash flow exchange if six-month MRR is set at 1.95%.

The financial intermediary owes Fyleton a fixed cash flow payment of GBP2,250,000 (= GBP200 million × 0.0225/2).
Fyleton owes the financial intermediary a floating cash flow payment of GBP1,950,000 (= GBP 200 million × 0.0195/2).
The fixed and floating payments are netted against one another, and the net result is that the financial intermediary pays Fyleton GBP300,000 (= GBP2,250,000 – GBP1,950,000).

5. Options

We now move to the other major category of derivative instruments called contingent claims. The holder of a contingent claim has the right, but not the obligation to make a final payment contingent on the performance of the underlying. Options are the most common type of contingent claims.

Options

An option is a derivative contract in which one party, the buyer, pays a sum of money to the other party, the seller or writer, and receives the right to either buy or sell an underlying asset at a fixed price either on a specific expiration date or at any time prior to the expiration date. Options trade on exchanges, or they can be customized in the OTC market.

The buyer/holder of an option is said to be long.

The seller/writer of an option is said to be short.

There are two types of options based on when they can be exercised:

European option: This type of option can be exercised only on the expiration date.
American option: This type of option can be exercised on or any time before the option’s expiration date.

There are two types of options based on the purpose it serves:

Call option: Gives the buyer the right to buy the underlying asset at a given price on a specified expiration date. The seller of the option has an obligation to sell the underlying asset.
Put option: Gives the buyer the right to sell the underlying asset at a given price on a specified expiration date. The seller of the option has an obligation to buy the underlying asset.

Assume there are two parties: A and B. A is the seller, writer, or the short party. B is the buyer or the long party. A and B sign a contract, according to which B has the right to buy one share of Strong Steel Inc. for $50 after six months.

In our example, B has bought the right to buy, which is called a call option. The right to sell is called a put option. If B has the right to buy a share (exercise the option) of Strong Steel Inc. anytime between now and six months, then it is an American-style option. But if he can exercise the right only at expiration, then it is a European-style option. $50, the price fixed at which the underlying share can be purchased, was fixed at inception and is called the strike price or exercise price.

B bought the right to buy the share at expiration from A. So, B has to pay A, a sum of money called the option premium for holding this right without an obligation to purchase the share.

The call premium B paid is $3. An investor would buy a call option if he believes the value of the underlying would increase.

The diagram below shows the call option payoff and profit for both a buyers and sellers perceptive.

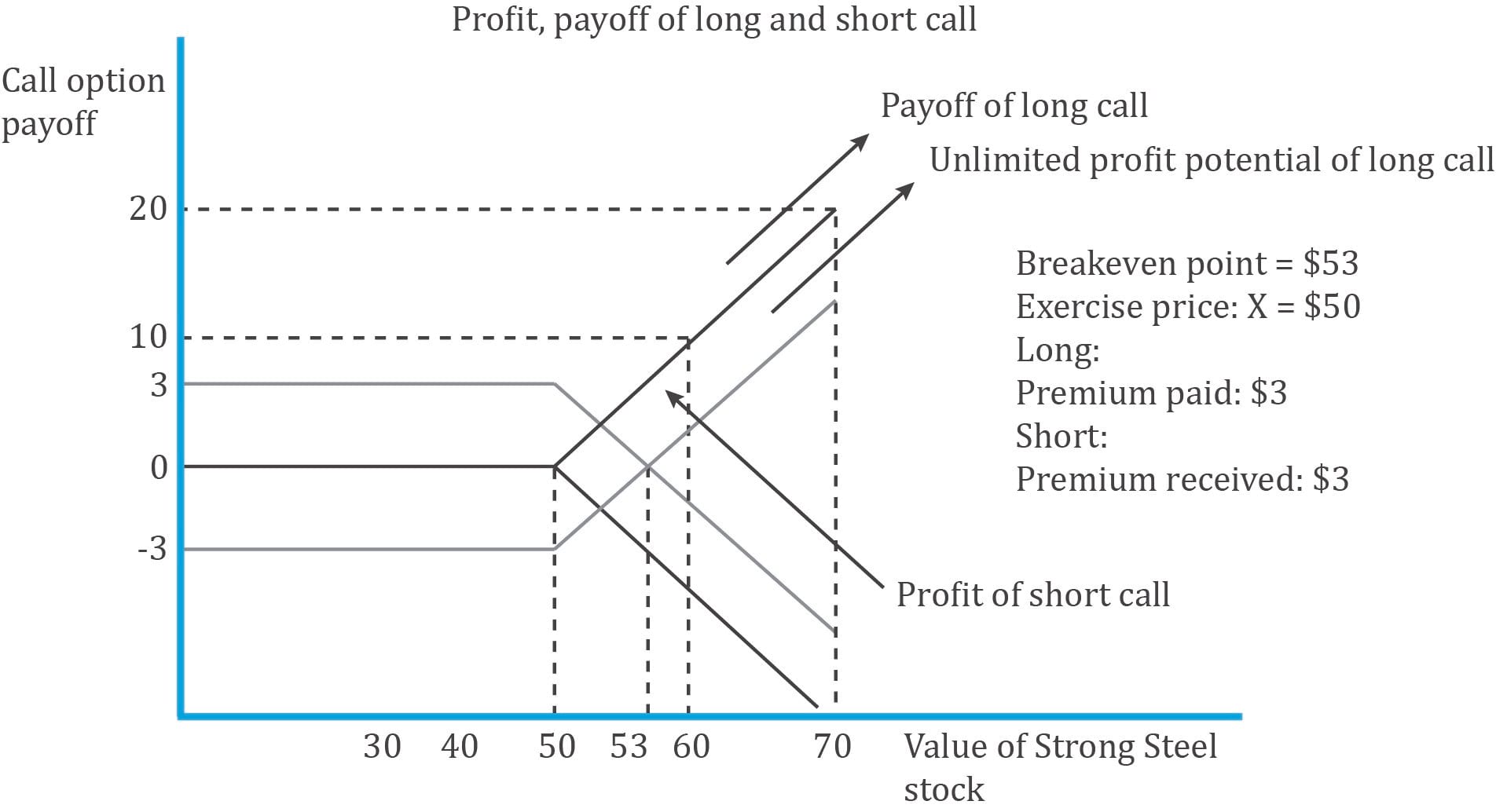
Call option buyer and seller payoff at expiration:

c_T = Max (0,S_T – X)

where:

S_T = stock’s price

X = exercise price

For example, suppose you buy a call option with an exercise price of 30 and an expiration of three months for a premium of 1.00 when the stock is trading at 25. At expiration, consider the outcomes when the stock’s price is 25, 30, or 35. The buyer’s payoffs would be:

For S_T = 25, payoff = c_T = Max(0,S_T – X) = Max(0,25 – 30) = Max(0, –5) = 0.

For S_T = 30, payoff = c_T = Max(0,S_T – X) = Max(0,30 – 30) = Max(0, 0) = 0.

For S_T = 35, payoff = c_T = Max(0,S_T – X) = Max(0,35 – 30) = Max(0, 5) = 5.

To the seller, who received the premium at the start, the payoff is:

–c_T = –Max(0,S_T – X)

At expiration, the call seller’s payoffs are:

For S_T = 25, payoff = –c_T = –Max(0,S_T – X) = –Max(0,25 – 30) = 0.

For S_T = 30, payoff = –c_T = –Max(0,S_T – X) = –Max(0,30 – 30) = 0.

For S_T = 35, payoff = –c_T = –Max(0,S_T – X) = –Max(0,35 – 30) = –5.

The call buyer’s profit would be:

Profit = Max(0,S_T – X) – c₀

where:

c₀ = option premium

For S_T = 25, profit = Max(0,S_T – X) – c₀ = Max(0,25 – 30) – 1.00 = – 1.

For S_T = 30, profit = Max(0,S_T – X) – c₀ = Max(0,30 – 30) – 1.00 = – 1.00.

For S_T = 35, profit = Max(0,S_T – X) – c₀ = Max(0,35 – 30) – 1.00 = 4.00.

The call seller’s profit is:

Π = –Max(0,S_T – X) + c₀

At expiration, the call seller’s profit for each underlying price at expiration are:

For S_T = 25, profit = –Max(0,S_T – X) + c₀ = –Max(0,25 – 30) + 1.00 = 1.00.

For S_T = 30, profit = –Max(0,S_T – X) + c₀ = –Max(0,30 – 30) + 1.00 = 1.00.

For S_T = 35, profit = –Max(0,S_T – X) + c₀ = –Max(0,35 – 30) + 1.00 = –4.00.

Put option buyer and seller payoff at expiration:

An investor would buy a put option if he believes the value of the underlying would decrease. If it decreases by expiration date, the investor has a right to exercise the option to sell the underlying at the exercise price, which will be greater than the then market price.

The payoff to the put holder is:

p_T = Max(0,X – S_T)

The put buyer’s profit would be:

Π = Max(0,X – S_T) – p₀

where: p₀ is option premium.

The payoff for the seller is:

–p_T = –Max(0,X – S_T)

The put seller’s profit would be:

Π = –Max(0,X – S_T) + p₀

Intrinsic value and time value of options

A call option is in-the-money when the price of the underlying is higher than the exercise price (i.e. S_t > X). It is out-of-the-money if (S_t < X) and at-the-money if (S_t = X).

Example: On 15 November, a 90-day European-style call option with an exercise price of $50.00 is priced at $4.60. The underlying is trading at $53.00. Hence, T = 90/365, S₀ = 53.00, X = 50.00, and c₀ = 4.60.

The option price has two components: 1) an exercise value component, also called intrinsic value, and 2) a time value component. Hence, we can say: c = exercise value + time value.

For a call option, the exercise value component is S – X if S > X. In our example, the exercise value is 53.00 – 50.00 = 3.00.
The time value component is equal to the option price minus that exercise value: 4.60 – 3.00 = 1.60.

The longer the time to expiration the higher the time value. The time value declines as time passes and becomes equal to zero at option expiration. At expiration, call and put values are equal to their intrinsic value or exercise value.

Counterparty credit risk

Options have one-sided counterparty credit risk. The option seller has no credit exposure to the option buyer after the premium is paid. However, the option buyer faces the counterparty credit risk of the option seller equal to the option payoff at maturity.

6. Credit Derivatives

A credit derivative is a class of derivative contracts between two parties, a credit protection buyer and a credit protection seller, in which the latter provides protection to the former against a specific credit loss. The main type of credit derivative is a credit default swap.

Credit Default Swap

A credit default swap is a derivative contract between two parties, a credit protection buyer and a credit protection seller, in which the buyer makes a series of cash payments to the seller and receives a promise of compensation for credit losses resulting from the default of a third party.

A CDS is a form of insurance.
The objective of a CDS is to buy protection to cover the loss of par value of the bond, if a credit event occurs. A credit event is like bankruptcy, restructuring, or failure to pay that impairs the borrower’s ability to make timely payments.
The CDS transfers the credit risk of the borrower from one party (protection buyer) to another (protection seller).
Credit migration: If the borrower’s credit spread widens (i.e. credit quality worsens) the CDS buyer has a MTM gain and the CDS seller has a MTM loss. The CDS MTM change is calculated as: Δ CDS spread x Notional x EffDur_CDS
Credit event: If the borrower defaults, the CDS seller pays the CDS buyer and the CDS contract terminates. The contingent payment is equal to the issuer Loss given default (LGD)% x the notional amount.

7. Forward commitments vs contingent claims

Market participants frequently create similar exposures to an underlying using different derivative instrument types. For example, both a long forward position and a call option position will benefit from an increase in the price of the underlying.

Exhibit 11 from the curriculum contrasts the payoff profiles of these two positions.

The profit for the forward contract is simply: S_T – F₀(T)

If the exercise price of the call option is set to F₀(T), the profit for the call option is:

Π = max[0, S_T– F₀(T)] – c₀.

Based on this, we can draw the following conclusions:

S_T – F₀(T) > –c₀ Forward profit exceeds option profit
S_T – F₀(T) = –c₀Forward profit equals call option profit
S_T – F₀(T) < –c₀Option profit exceeds forward profit

When the stock price moves up the profits are similar. But when the stock price moves down, the call option provides downside protection in exchange for paying a premium.