This learning module covers:
According to the ‘law of one price’ two identical assets should trade at the same price. An arbitrage opportunity exists if the ‘law of one price’ does not hold.
In case of derivatives arbitrage opportunities exist when:
Scenario 1
Exhibit 1 from the curriculum illustrates the first scenario.
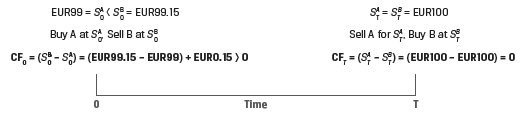
Consider two zero-coupon bonds A and B. Both bonds are from the same issuer, have identical features, and will mature on the same future date.
Since two assets with identical future cash flows trade at different prices, the ‘law of one price’ is violated and an arbitrage opportunity exists.
At time t = 0, an investor can:
At time t = T, when both bonds mature, the investor:
Other market participants will also exploit this opportunity, selling Bond B, driving its price down, and buying Bond A, driving its price up, until the prices converge.
Scenario 2
The second-type of derivative-related arbitrage opportunity arises when an asset with a known future price does not trade at the PV of its future price.
In an earlier reading on time-value-of-money, we learnt that the future value of a single cash flow can be calculated based on discrete compounding or continuous compounding.
The FV based on discrete compounding is:
FVN = PV(1 + r)N
The FV based on continuous compounding is:
FVT = PVerT
Both approaches can be used for pricing derivatives. The curriculum uses the discrete compounding method for individual underlying assets (e.g. a stock); and the continuous compounding method for underlying assets that represent a portfolio (e.g. an equity index) or where the underlying involves foreign exchange.
The following example from the curriculum demonstrates how an arbitrage profit can be earned in scenario 2.
Example: Spot vs. Discounted Known Future Price of Gold
(This is based on Example 1 from the curriculum.)
A company entered into a contract to buy 100 ounces of gold at an agreed-upon price of USD1,792.13 per ounce in three months.
Assume that today’s spot gold price (S0) is USD1,770 per ounce, and the annualized risk-free interest rate (r) is 2%. Also assume that the company can borrow at the risk-free rate and there are no additional costs or benefits associated with gold ownership. Under these conditions demonstrate how the company can generate a riskless profit.
Solution:
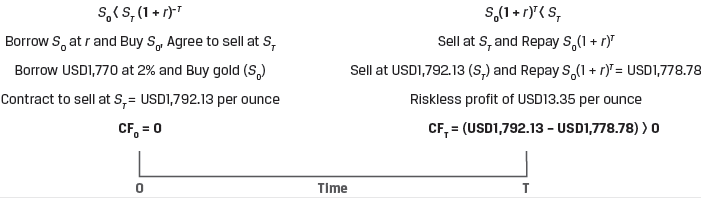
At time t = 0,
At time t = T (in three months),
In this example, the spot price of gold is below the PV of the known futures price in three months. Other market participants will also exploit this arbitrage opportunity by purchasing gold in the spot market and selling it in the forward market. This will cause the spot price to increase and the forward price to fall until the arbitrage opportunity is eliminated.
Instructor’s Note: The two scenarios demonstrate that arbitrage opportunities will be exploited by market participants and the prices will quickly adjust. Therefore, while pricing derivative we set a price such that no arbitrage opportunities exist.
The two key arbitrage concepts used to price derivatives for an underlying with no additional cash flows are:
The relationship between spot prices, forward commitment prices, and the risk-free rate is shown in Exhibit 2.

For a given time T, the higher the risk-free rate (r), the higher the forward price.
For a given risk-free rate, the longer the time period (T), the higher the forward price.
Replication is a strategy in which a derivative’s cash flow stream may be recreated using a combination of long or short positions in an underlying asset and borrowing or lending cash.
Example 2 from the curriculum, demonstrates how a forward commitment can be replicated by purchasing the underlying asset in the spot market using funds borrowed at the risk-free rate.
Example: Replication of a Forward Commitment
(This is based on Example 2 from the curriculum.)
Using the same data as Example 1, now assume that the spot price of gold has risen to USD1,783.28 so that the arbitrage opportunity is eliminated. Assume again that the risk-free interest rate (r) is 2% and gold can be stored at no cost.

Two equivalent choices available to an investor are:
When the forward contract is priced such that no arbitrage opportunity exists (F0(T) = S0(1 + r)T), both choices will result in the same payoff, i.e., we can say that a forward commitment can be replicated buy purchasing the underlying asset in the spot market using borrowed funds.
Derivatives can also be used to replicate a risk-free rate. When a long cash position is combined with a short forward position, the investor will earn a risk-free rate of return. This is demonstrated in Example 3 from the curriculum.
Example: Risk-Free Trade Replication: Long Asset, Short Forward
(This is based on Example 3 from the curriculum.)
A company buys 100 ounces of gold at today’s spot price (S0) of USD1,783.28 and simultaneously enters a forward commitment to sell gold at the forward price, F0(T), of USD1,792.13.
At t = 0, the company’s cash flow is –S0 = –USD178,328.
At t = T, the company’s cash flow is F0(T) = USD179,213.
Solve for the rate of return on this strategy, as follows:
USD179,213 = USD178,328(1 + r)0.25.
r = 2.0%, which is equal to the risk-free rate.
So far in our discussion we assumed that the underlying asset had no additional associated cash flows and the forward prices were established as:
F0(T) = S0(1 + r)T under discrete compounding and
F0(T) = S0erT under continuous compounding
In these formulas, the risk-free rate r denotes the opportunity cost of holding the asset. If the investor had not purchased the asset, he could have earned the risk-free rate instead. Therefore, the forward price should be such that the investor is compensated for bearing this cost.
Now, we will relax our assumptions and consider the additional costs and benefits associated with owning underlying assets. Examples of costs of ownership include storage, transportation, insurance and spoilage costs. Examples of benefits of ownership include dividends and coupons.
Refer to Exhibit 7 from the curriculum.
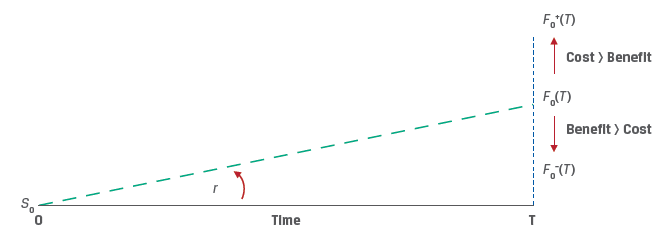
If the underlying asset owner incurs cost in addition to the opportunity costs, the forward price should be higher to compensate investors. On the other hand, if the underlying asset provides benefits the forward price will be lower.
Cost of carry is the net cost of holding an asset, Cost of carry = Cost – Benefits.
The relationship between spot and forward prices for an underlying asset with ownership benefits/income (I) and costs (C) can be expressed as:
F0(T) = [S0 – PV0(I) + PV0(C)](1 + r)T
Sometimes, the additional costs or benefits are expressed as a rate of return instead of absolute amounts. For income (i) and cost (c) expressed as rates of return, the relationship between spot and forward prices under continuous compounding is:
F0(T) = S0e(r+c–i)T
Exhibit 8 illustrates the relationship between forward and spot prices in the presence of costs and benefits.

Example: Equity Forward with Dividend
(This is based on Example 4 from the curriculum.)
A company enters into a forward contract to deliver 1,000 shares of Unilever (UL) in six months. UL has a spot price of EUR50. It pays a quarterly dividend of EUR0.30, which occurs in exactly three months and again at time T. The risk-free rate is 5%. Calculate the forward price F0(T), in six months.
Solution:
The forward price can be calculated as:
F0(T) = [S0 – PV0(I) + PV0(C)](1 + r)T.
As per the data provided, there are no costs in owning UL, therefore PV0(C) = 0
PV0(I) is the present value of the dividend per share. It can be calculated as:
PV0(I) = EUR0.30(1.05)–0.25 + EUR0.30(1.05)–0.5.
PV0(I) = 0.2964 + 0.2928 = EUR0.5892.
Therefore, F0(T) = (EUR50 – EUR0.5892)(1.05)0.5 = EUR50.6310.
Example: Stock Index Futures with Dividend Yield
(This is based on Example 5 from the curriculum.)
An investor would like to enter into a three-month forward commitment contract to purchase the NIFTY 50 benchmark Indian stock market index. The spot NIFTY 50 index price is INR15,200, the index dividend yield is 2.2%, and the Indian rupee risk-free rate is 4%. Calculate the forward price. (Assume c = 0)
Solution:
The forward price can be calculated as:
F0(T) = S0e(r+c–i)T
= 15,200e(0.04 – 0.022)0.25
= INR15,268.55.
FX (foreign exchange) Forward Contracts
An FX (foreign exchange) forward contract involves the sale of one currency and purchase of the other on a future date at a forward price (F0,f/d) agreed on at inception.
A long FX forward position involves the purchase of the base currency and the sale of the price currency. For example, a long USD/EUR FX forward position involves purchasing Euros and selling US dollars at a forward rate.
The no-arbitrage condition FX forward rate can be calculated as:
F0(T) = S0 e(rf-rd)T
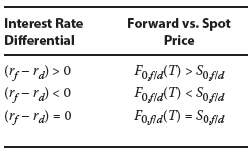
Instructors Note: Foreign exchange is a special case in which the cost of carry is the interest rate differential between the foreign and domestic risk-free rates (rf – rd).
Exhibit 9 from the curriculum illustrates the relationship between FX Forward and spot rates.
Example:
(This is Knowledge check example 4 from the curriculum.)
An analyst observes that the current spot MXN/USD exchange rate is 19.50, the Mexican peso six-month risk-free rate is 4%, and the six-month US dollar risk free rate is 0.25%. Describe the relationship between the MXN/USD spot and six-month forward rate.
Solution:
The interest rate differential (rf – rd) > 0 calculates as (4% – 0.25% = 3.75%). Therefore, we can expect the forward rate to be higher than the spot rate.
The forward rate can be calculated as:
F0(T) = S0 e(rf-rd)T
F0(T) = 19.50 e(4%–0.25%)0.5 = 19.8691
Convenience Yield
Convenience yield refers to a non-cash benefit of holding a physical commodity versus a derivative. Sometimes economic conditions may arise that cause market participants to prefer to own physical commodities. For example, if crude oil inventories are very low, refineries may bid up the spot oil price so that forward prices do not fully reflect storage costs and interest rates.