This learning module covers:
Futures are standardized, exchange-traded derivatives (ETDs) with zero initial value and a futures price f0(T) established at inception.
Instructor’s Note: Small letter ‘f’ is used for futures and capital letter ‘F’ is used for forwards. The calculation of futures price is similar to the calculation of forward price covered in the previous reading.
The futures price for an underlying asset with no cost or benefit is calculated as:
f0(T) = S0(1 + r)T
As with forwards, discrete compounding is used for futures on individual assets. However, if the underlying asset comprises a portfolio-such as equity, fixed income, commodity or credit index; or if the underlying involves foreign exchange, continuous compounding is used. The futures price is calculated as:
f0(T) = S0erT
The futures price for an underlying asset with ownership benefits or income (I) and costs (C) is calculated as:
f0(T) = [S0 – PV0(I) + PV0(C)] (1 + r)T
Marking to market: Futures contracts are marked to market on a daily basis. What this means is that if there is a gain or loss on the position relative to the previous day’s closing price, then the gain is credited to the winning account by deducting the amount from the losing account.
So unlike a forward contract, where the gain or loss is realized at the end of the contract period; in a futures contract, there is a cash flow on a daily basis. This daily settlement resets the futures contract value to zero every day and the process continues until contract maturity when the futures price converges to the spot price ST.
The cumulative realized mark-to-market (MTM) gain or loss on a futures contract is approximately the same as for a comparable forward contract. However, while the forward contract price, F0(T) remains fixed until the contract matures, future contract prices fluctuate daily based on market changes.
The following example will help understand these concepts.
Example:
Assume that the spot price of a stock is $100, and that a three-period futures contract on this stock has a price of $115. An equivalent forward contract expiring in three periods also has a price of $115. The following table shows the cash flows to long and short parties of these contracts as the price of the stock’s future contract changes:
| Time period | Future contract price | Forward contract price | Long Forward Cash Flow | Short Forward Cash Flow | Long Future Cash Flow | Short Future Cash Flow |
| 0 | $115 | $115 | – | – | – | – |
| 1 | $120 | $115 | $0 | $0 | $5 | -$5 |
| 2 | $130 | $115 | $0 | $0 | $10 | -$10 |
| 3 | $125 | $115 | $10 | -$10 | -$5 | $5 |
| Net | $10 | -$10 | $10 | -$10 |
In both cases, the net cash flow from seller to buyer is $10, but the timing of the cash flows is different. The settlement of a forward contract occurs at maturity. But the profits or losses are recorded on the futures contract at the end of each period.
Also, the forward price remains fixed at $115, but the futures price varies each period.
In the previous reading, we learnt that zero rates can be used to calculate the implied forward rate, and that the implied forward rate is used to set the fixed rate on a forward rate agreement (FRA).
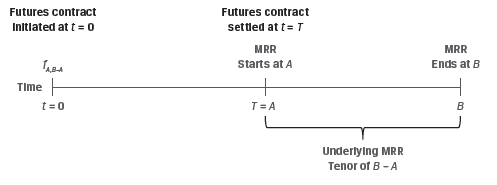
Interest rate futures offer investors a highly liquid and standardized alternative to FRA. Like FRAs, the underlying for interest rate futures is the market reference rate (MRR) on a hypothetical deposit. However, interest rate futures trade on a price basis, as per the following formula:
fA,B−A = 100 − (100 × MRRA,B−A)
where fA,B−A represents the futures price for a market reference rate for B−A periods that begins in A periods (MRRA,B−A)
This is illustrated in Exhibit 3 from the curriculum.
The interest rate futures price can be used to calculate the implied MRR. For example, we may solve for the implied three-month MRR rate in three months’ time (where A = 3m, B = 6m, B − A = 3m) if an interest rate futures contract is trading at a price of 98.25.
f3m,3m: 98.25 = 100 − (100 × MRRA,B−A)
MRR3m,3m = 1.75%.
This (100-yield) price convention results in an inverse price/yield relationship that is different from an FRA. A long futures contract gains as price rises i.e. the future MRR falls. Whereas, a short futures contract gains as the price falls i.e. future MRR rises.
Exhibit 4 from the curriculum summarizes the relationship between interest rate futures and FRAs.
| Contract Type | Gains from Rising MRR | Gains from Falling MRR |
| Interest rate futures | Short futures contract | Long futures contract |
| FRA | Long FRA: FRA fixed-rate payer | Short FRA: FRA floating-rate payer |
The daily settlement of interest rate futures is based on price changes, which translate into futures contract basis point value (BPV) as follows:
Futures Contract BPV = Notional Principal × 0.01% × Period
For example, assuming a $1,000,000 notional for three-month MRR of 2.21% for one quarter (or 90/360 days), the underlying deposit contract value would be:
$1,005,525 = $1,000,000 × [1 + (2.21% / 4)].
Consider how a one basis point (0.01%) change in MRR affects contract value:
1 bp increase (2.22%): $1,005,550 = $1,000,000 × [1 + (2.22% / 4)].
1 bp decrease (2.20%): $1,005,500 = $1,000,000 × [1 + (2.20% / 4)].
Both the increase and decrease in MRR by one basis point change the contract BPV by $25. Thus, short-term interest rate futures exhibit a fixed linear relationship between price and yield changes.
Forward and future prices are identical if:
A violation of these assumptions can give rise to differences in pricing between these two contracts.
There is a price difference between interest rate futures and FRAs due to the convexity bias. This is illustrated in the following example.
Example: Interest Rate Forwards versus Futures
(This is Example 5 from the curriculum.)
Let us return to an earlier example with an interest rate futures contract of $1,000,000 notional for three-month MRR of 2.21% for one quarter (or 90/360 days). Recall that the underlying deposit contract value was:
$1,005,525 = $1,000,000 × [1 + (2.21% / 4)].
The contract BPV was shown to be $25 (= $1,000,000 × 0.01% × [1/4]).
Consider in contrast a $1,000,000 notional FRA on three-month MRR in three months’ time with an identical 2.21% rate. The net payment on the FRA is based upon the difference between MRR and the implied forward rate (IFR):
Net Payment = (MRRB−A − IFRA,B−A) × Notional Principal × Period.
For example, if the observed MRR in three months is 2.22% (+0.01%), the net payment at maturity would be $25 (= $1,000,000 × 0.01% × [1/4]). However, the settlement of an FRA is based upon the present value of the final cash flow discounted at MRR, so:
Cash Settlement (PV): $24.86 = $25 /(1 + 0.0222 / 4).
If we increase the magnitude of the MRR change at settlement and compare these changes between a long interest rate futures position and a short receive-fixed (pay floating) FRA contract, we arrive at the following result:
| MRR3m,3m | Short FRA Cash Settlement (PV) | Long Futures Settlement |
| 2.01% | $497.50 | $500 |
| 2.11% | $248.69 | $250 |
| 2.21% | $0 | $0 |
| 2.31% | ($248.56) | ($250) |
| 2.41% | ($497.01) | ($500) |
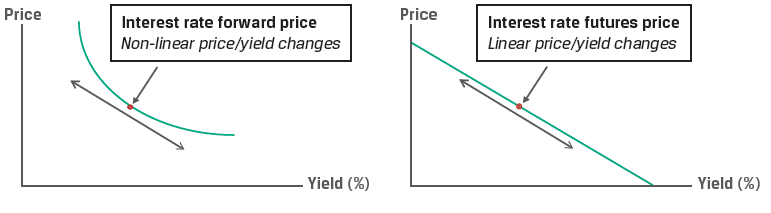
Note that while the futures contract has a fixed linear payoff profile for a given basis point change, the FRA settlement does not.
The discounting feature of the FRA, which is not present in the futures contract, leads to a convexity bias, as illustrated in Exhibit 5.
The advent of derivatives central clearing has introduced futures-like margining requirements for OTC derivatives dealers who buy and sell forwards to derivatives end users. Dealers who must post cash or highly liquid securities to a central counterparty often impose similar requirements on derivatives end users. This is illustrated in Exhibit 6 from the curriculum.

These margin requirements have reduced the difference in the cash flow impact of ETDs and OTC derivatives. Therefore, the price difference between futures and forwards has also reduced.