LM07 Pricing and Valuation of Interest Rates and Other Swaps

Part 1

1. Introduction

This learning module covers:

• How swap contracts are similar to but different from a series of forward contracts
• Valuation and pricing of swaps

2. Swaps vs. Forwards

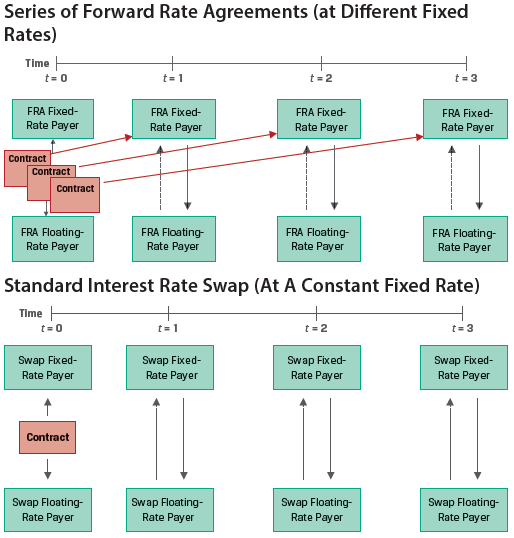
A swap contract is an agreement between two counterparties to exchange a series of future cash flows, while a forward contact is an agreement for a single exchange of value at a future date.

How do Swaps work?

To understand how swaps work, let us consider a 3-year plain vanilla interest rate swap with annual settlement where the fixed-rate payer pays 10% and the floating rate payer pays an interest based on MRR. Also  assume that the future MRR rates at t = 0, 1, and 2 are 9%, 10%, and 11%.

At times 0, 1, and 2, the two parties exchange a series of payments. The fixed rate payer makes a fixed payment of 10% and receives a floating payment based on the value of the underlying at that point in time. Here is it 9%, 10%, and 11% respectively.

The payments are netted. At t=1, the fixed rate payer will make a payment of 1% of notional principal to the floating rate payer. At t=2 no cash flows will be exchanged. At t=3, the floating rate payer will make a payment of 1% of notional principal to the fixed rate payer.

Similarities between FRAs and Swaps

• Both FRAs and swaps allow users to lock-in a fixed rate for future. In both cases, the net difference between a fixed rate agreed upon at inception and a future MRR is used to determine cash settlement.
• Both FRAs and swaps have a symmetric payoff profile.
• No cash is exchanged upfront. Both have a value of 0 at initiation.
• Both FRAs and swaps involve counterparty credit exposure.

Differences between FRAs and Swaps

• An FRA has a single settlement, which occurs at the beginning of an interest period, while a swap has periodic settlements, which occur at the end of each respective period.
• A swap contract is like a series of FRAs, where each FRA has a different time to maturity. While a swap has a constant fixed rate over its life, the series of FRAs will have different fixed rates for different times to maturity. This is illustrated in Exhibit 2 from the curriculum.

• Financial intermediaries often use FRAs to manage interest rate exposure. But derivative end users, such as issuers and investors, usually prefer swaps because they better match rate-sensitive assets and liabilities with periodic cash flows, such as fixed-coupon bonds, variable rate loans, or known future commitments.

Calculating the Swap Rate

The following example demonstrates how to calculate the swap rate.

Example: Swaps as a Combination of Forwards

(This is based on Example 1 from the curriculum.)

Suppose we are provided the following data:

As shown in a previous reading, using the zero rates we can calculate the implied one period forward rates.

IFR_0,1 = (1.023960) – 1 =2.3960%

IFR_1,1 = (1.034197)²/(1.02396) – 1 = 4.4536%

IFR_2,1 = (1.040005)³/(1.034197)² – 1 = 5.1719%

The par swap rate is the fixed rate that equates the present value of all future expected floating cash flows to the present value of fixed cash flows.

Σ PV(Floating payments) = Σ PV(Fixed payments), or

IFR/(1+z_i)ⁱ =   s_i/(1+z_i)ⁱ
In our example,
+ + = + +

+ + = + +
0.111017 = 2.800545 × s3.
s3 = 3.9641%.

The three-year swap rate of 3.9641% calculated in the above example can be interpreted as a multiperiod breakeven rate at which an investor will be indifferent to:

• paying the fixed swap rate and receiving the respective forward rates or
• receiving the fixed swap rate and paying the respective forward rates.

Therefore, the fixed swap rate can be thought of as an internal rate of return on the implied forward rates over the life of the swap.

Using Swaps to Manage Fixed-Income Exposure

A pay fixed receive floating swap is similar to going long a floating rate bond and going short a fixed rate bond. This is illustrated in Exhibit 4 from the curriculum.

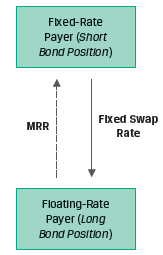
Because swaps are more liquid than individual bond positions, active fixed-income portfolio managers often use swaps rather than underlying securities to adjust their interest rate exposure.

For example, if interest rates are expected to fall, a portfolio manager may choose to receive fixed on a swap rather than purchase underlying bonds in order to profit from the lower rate environment.

Instructor’s Note: A receive fixed swap will benefit when interest rates decline. A pay fixed swap will benefit when interest rates rise.

3. Swap Values and Prices

The swap price is the swap fixed rate determined at contract initiation.

The value of the swap is zero at initiation, but its value changes as time passes and interest rates change.

The periodic settlement for a fixed-rate payer on a swap can be calculated as:

Periodic settlement value = (MRR – swap fixed rate) × Notional amount × Period

The value of a swap on any settlement date equals the current settlement value plus the present value of all remaining future swap settlements.

If the MRR at a settlement date is higher than the expected forward rate (IFR), the PV of floating rate payments will be higher than the PV of fixed rate payments, causing an MTM gain for the fixed-rate payer and an MTM loss for the fixed-rate receiver.

Share on :