We use the following table to decide which test statistic and which corresponding probability distribution to use for hypothesis testing.
| Sampling from | Small sample size | Large sample size | |
| Normal distribution | Variance known | z | z |
| Variance unknown | t | t (or z) | |
| Non–normal distribution | Variance known | NA | z |
| Variance unknown | NA | t (or z) | |
You believe that the average returns of all stocks in the S&P 500 is greater than 10%. You draw a sample of 49 stocks. The average return of these 49 stocks is 12%. The standard deviation of returns of all stocks in the S&P 500 is 4%. Using a 5% level of significance, determine if your belief is correct.
Solution:
Step 1: State the hypothesis
H0: µ ≤ 10%
Ha: µ > 10%
Step 2: Calculate the test statistic
The population variance is known hence we will use z-statistic.
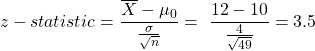
Step 3: Calculate the critical value
This is a one-tailed test and we will be looking at the right tail. Using the Z –table and 5% level of significance
Critical value = Z0.05 = 1.65
Step 4: Decision
Since the test statistic (3.5) > critical value (1.65), we reject H0. Hence at 5% level of significance, your belief that the average returns of all stocks in the S&P 500 is greater than 10% is correct.
You believe that the average returns of all stocks in the S&P 500 is greater than 10%. You draw a sample of 25 stocks. The average return of these 25 stocks is 12% and the standard deviation of their returns is 7%. Using a 5% level of significance, determine if your belief is correct.
Solution:
Step 1: State the hypothesis
H0: µ ≤ 10%
Ha: µ > 10%
Step 2: Calculate the test statistic
The population variance is not known hence we will use t-statistic.
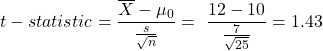
Step 3: Calculate the critical value
This is a one-tailed test and we will be looking at the right tail. Using the t –table and 5% level of significance and degrees of freedom = 25 -1 = 24
Critical value = t24,0.05= 1.71
Step 4: Decision
Since the test statistic (1.43) < critical value (1.71), we cannot reject H0. Hence at 5% level of significance, your belief that the average returns of all stocks in the S&P 500 is greater than 10% is incorrect.