101 Concepts for the Level I Exam

Concept 12: Calculating Confidence Intervals

To calculate a confidence interval for a population mean, follow these steps:

Refer to the table below and select t statistic or z statistic as per the scenario.

Sampling from		Small sample size	Large sample size
Normal distribution	Variance known	z	z
Normal distribution	Variance unknown	t	t (or z)
Non–normal distribution	Variance known	NA	z
Non–normal distribution	Variance unknown	NA	t (or z)

Use the following formulae to calculate the confidence interval:

$Confidence\ interval=\ \overline{X}\pm \ z_{\alpha /2\ \ }{{\sigma }\over {\sqrt{n}}}$$ $$Confidence\ interval=\ \overline{X}\pm \ t_{\alpha /2\ \ }{{s}\over {\sqrt{n}}}$

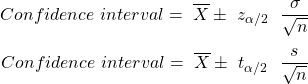
For a Z distribution,

90% confidence à critical value = 1.65

95% confidence à critical value = 1.96

99% confidence à critical value = 2.58

You take a random sample of 100 large cap stocks. The average returns of these stocks for the past year is 12%. Assume that the average returns for all large-cap stocks in the economy follow a normal distribution with a standard deviation of 3%. Construct a 99% confidence interval for the average return all large-cap stocks for the past year.

Solution:

Since the population variance is known (the standard deviation of all large cap stocks), we will use Z statistic.

For confidence level of 99%, 1% error in both tails i.e. 0.5% (0.005) in one tail. Z_α/2 = Z_0.005 = 2.58 (From Z-table)

The confidence interval can be calculated as

$\noindent $Confidence\ interval=\ 12\pm \ 2.58{{3}\over {\sqrt{100}}}$ = 11.226 to 12.774$

You construct a sample of monthly returns of Stock A for the past two years. The stock has a mean return of 2% and a standard deviation of 8%. Compute the 95% confidence interval for the average monthly returns for this stock.

Solution:

Since the population variance is unknown (the variance of monthly returns of Stock A over its entire history, we only have data for the past two years) we will use t statistic.