IFT Notes for Level I CFA^® Program

LM05 Sampling and Estimation

Part 2

4. Point Estimates of the Population Mean

Statistical inference consists of two branches: 1) hypothesis testing and 2) estimation. Hypothesis testing addresses the question ‘Is the value of this parameter equal to some specific value?’ This is discussed in detail in the next reading. In this section, we will discuss estimation. Estimation seeks to answer the question ‘What is this parameter’s value?’ In estimation, we make the best use of the information in a sample to form one of several types of estimates of the parameter’s value.

A point estimate is a single number that estimates the unknown population parameter.

Interval estimates (or confidence intervals) are a range of values that bracket the unknown population parameter with some specified level of probability.

4.1. Point Estimators

The formulas that we use to compute the sample mean and all other sample statistics are examples of estimation formulas or estimators. The particular value that we calculate from sample observations using an estimator is called an estimate. For example, the calculated value of the sample mean in a given sample is called a point estimate of the population mean.

The three desirable properties of an estimator are:

Unbiasedness: Its expected value is equal to the parameter being estimated.
Efficiency: It has the lowest variance as compared to other unbiased estimators of the same parameter.
Consistency: As sample size increases, the sampling error decreases and the estimates get closer to the actual value.

5. Confidence Intervals for the Population Mean and Sample Size Selection

A confidence interval is a range of values, within which the actual value of the parameter will lie with a given probability. Confidence interval is calculated as:

Confidence interval = point estimate ± (reliability factor x standard error)

where:

point estimate = a point estimate of the parameter

reliability factor = a number based on the assumed distribution of the point estimate and the degree of confidence (1 – α) for the confidence interval

standard error = standard error of the sample statistic providing the point estimate

The quantity ‘reliability factor x standard error’ is also referred to as the precision of the estimator. Larger values indicate lower precision and vice versa.

Calculating confidence intervals

To calculate a confidence interval for a population mean, refer to the table below and select t statistic or z statistic as per the scenario.

Sampling from		Small sample size(n<30)	Large sample size(n≥30)
Normal distribution	Variance known	z	z
Normal distribution	Variance unknown	t	t (or z)
Non –normal distribution	Variance known	NA	z
Non –normal distribution	Variance unknown	NA	t (or z)

Use the following formulae to calculate the confidence interval:

$\rm Confidence \ Interval = \overline{X} + z_{\frac{\alpha}{2}}\times \frac{ \sigma}{\sqrt{n}}$

$\rm Confidence \ Interval = \overline{X} + t_{\frac{\alpha}{2}}\times \frac{s}{\sqrt{n}}$

Sampling from a normal distribution with known variance

The most basic confidence interval for the population mean arises when we are sampling from a normal distribution with known variance.

The confidence interval will be calculated as:

$\rm Confidence \ Interval = \overline{X} + z_{\frac{\alpha}{2}}\times \frac{ \sigma}{\sqrt{n}}$

where:

$\rm \overline{X}$ = sample mean

$\rm z_{\frac{\alpha}{2}}$ = reliability factor

$\rm \frac{ \sigma }{\sqrt{n}}$ = standard error

The reliability factor ( $z_{\frac{\alpha}{2}}$ ) depends purely on the degree of confidence. If the degree of confidence (1 – α) is 95% or 0.95, the level of significance (α) is 5% or 0.05. α/2 = 0.025. α/2 is the probability in each tail of the standard normal distribution. This is shown in blue in the figure below:

The reliability factors that are most frequently used when we construct confidence intervals based on the standard normal distribution are:

90% confidence intervals: α = 0.1, α/2 = 0.05. Reliability factor = z_0.5 = 1.65
95% confidence intervals: α = 0.05, α/2 = 0.025. Reliability factor = z_0.25= 1.96
99% confidence intervals: α = 0.01, α/2 = 0.005. Reliability factor = z_0.05 = 2.58

Memorize these confidence intervals and the corresponding reliability factors.

Example

You take a random sample of stocks on the National Stock Exchange (NSE). The sample size is 100 and the average Sharpe ratio is 0.50. Assume that the Sharpe ratios of all stocks on the NSE follow a normal distribution with a standard deviation of 0.30. What is the 90% confidence interval for the mean Sharpe ratio of all stocks on the NSE?

Solution:

$\rm Confidence \ Interval = \overline{X} \pm \ Z_{\frac{ \alpha}{2}} \times \frac{\sigma}{\sqrt{n}} = 0.50 \pm \ 1.65 \frac{0.30}{\sqrt{100}} = 0.50 \pm \ 0.0495$

Therefore, the 90% confidence interval for the mean Sharpe ratio of all stocks on the NSE is: 0.4505 to 0.5495.

As we increase the degree of confidence, the confidence interval becomes wider. If we use a 95% confidence interval, the reliability factor is 1.96. And the confidence interval ranges from 0.50 – 1.96 x 0.03 to 0.50 + 1.96 x 0.03 which is: 0.4412 to 0.5588. This range is wider than what we had with a 90% confidence interval.

Sampling from a normal distribution with unknown variance

If the distribution of the population is normal with unknown variance, we can use the t-distribution to construct a confidence interval.

The confidence interval can be calculated using the following formula:

$\rm Confidence \ Interval = \overline{X} + t_{ \frac{ \alpha }{2}} \frac{s}{\sqrt{n}}$

This relationship is similar to what we’ve discussed before except here we use the t-distribution. Since the population standard deviation is not known, we have to use the sample standard deviation which is denoted by the symbol ‘s’. We will now see how to read the t-distribution table using an example.

Example

Given a sample size of 20, what is the reliability factor for a 90% confidence level?

Solution:

In order to answer this question, we need to refer to the t-table. A snapshot of the table is given below. This table shows the level of significance for one-tailed probabilities.

df	P = 0.10	P = 0.05	P = 0.025	P = 0.01	P = 0.005
1	3.078	6.314	12.706	31.821	63.657
2	1.886	2.920	4.303	6.965	9.925
3	1.638	2.353	3.182	4.541	5.841
4	1.533	2.132	2.776	3.747	4.604
5	1.476	2.015	2.571	3.365	4.032
6	1.440	1.943	2.447	3.143	3.707
7	1.415	1.895	2.365	2.998	3.499
8	1.397	1.860	2.306	2.896	3.355
9	1.383	1.833	2.262	2.821	3.250
10	1.372	1.812	2.228	2.764	3.169
11	1.363	1.796	2.201	2.718	3.106
12	1.356	1.782	2.179	2.681	3.055
13	1.350	1.771	2.160	2.650	3.012
14	1.345	1.761	2.145	2.624	2.977
15	1.341	1.753	2.131	2.602	2.947
16	1.337	1.746	2.120	2.583	2.921
17	1.333	1.740	2.110	2.567	2.898
18	1.330	1.734	2.101	2.552	2.878
19	1.328	1.729	2.093	2.539	2.861
20	1.325	1.725	2.086	2.528	2.845

The degrees of freedom in this case are n – 1 = 20 – 1 = 19. The level of significance is calculated as: 100(1 – α) % = 90% and α = 0.10. In order to calculate the reliability factor t_a/2 = t_0.10/2= t_0.05, we look at the row with df = 19. We then look at the column with p = 0.05. The value that satisfies these two criteria is 1.729. This is the reliability factor.

Example

An analyst wants to estimate the return on the Hang Seng Index for the current year using the following data and assumptions:

Sample size = 64 stocks from the index
Mean return for the stocks in the sample for the previous year = 0.12
Variance = 0.081

It is given that the reliability factor for a 95% confidence interval with unknown population variance and sample size greater than 64 is 1.96. Assuming that the index return this year will be the same as it was last year, what is the estimate of the 95% confidence interval for the index’s return this year?

Solution:

$\rm Confidence\ Interval = \overline{X} + t_{\frac{\alpha}{2}} \frac{s}{\sqrt{n}} = 0.12 \pm 1.96 \times \frac{\sqrt{0.081}}{\sqrt{64}} = 0.12 \pm 0.07 = 0.05\ to\ 0.19$

Instructor’s Note:

A conservative approach to confidence intervals relies on the t-distribution rather than the normal distribution, and use of the t-distribution will increase the reliability of the confidence interval.

5.1 Selection of Sample Size

The choice of sample size affects the width of a confidence interval. A larger sample size decreases the width of a confidence interval and improves the precision with which we can estimate the population parameter. This is obvious when we consider the confidence interval relationship, shown below:

$\rm Confidence \ Interval = \overline{X} \pm \ t_{\frac{\alpha}{2}} \frac{s}{\sqrt{n}}$

All else being equal, when the sample size (n) is increased, the standard error (s/ ) decreases and we have a more precise (narrower) confidence interval. Based on this discussion it might appear that we should use as large a sample size as possible. However, we must consider the following issues:

Increasing the sample size may result in sampling from more than one population.
Increasing the sample size may involve additional expenses that outweigh the value of additional precision.

6. Resampling

Resampling is a computational tool in which we repeatedly draw samples from the original observed data sample for the statistical inference of population parameters. Two popular resampling methods are:

Bootstrap
Jackknife

Bootstrap

The bootstrap technique is illustrated in the figure below:

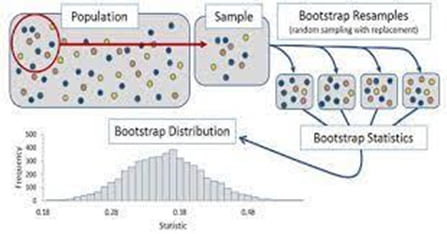
The technique is used when we do not know what the actual population looks like. We simply have a sample of size n drawn from the population. Since the random sample is a good representation of the population, we can simulate sampling from the population by sampling from the observed sample i.e., we treat the randomly drawn sample as if it were the actual population.

Under this technique, samples are constructed by drawing observations from the large sample (of size n) one at a time and returning them to the data sample after they have been chosen. This allows a given observation to be included in a given small sample more than once. This sampling approach is called sampling with replacement.

If we want to calculate the standard error of the sample mean, we take many resamples and calculate the mean of each resample. We then construct a sampling distribution with these resamples. The bootstrap sampling distribution will approximate the true sampling distribution and can be used to estimate the standard error of the sample mean. Similarly, the bootstrap technique can also be used to construct confidence intervals for the statistic or to find other population parameters, such as the median.

Bootstrap is a simple but powerful technique that is particularly useful when no analytical formula is available to estimate the distribution of estimators.

Jackknife

In the Jackknife technique we start with the original observed data sample. Subsequent samples are then created by leaving out one observation at a time from the set (and not replacing it). Thus, for a sample of size n, jackknife usually requires n repetitions. The Jackknife method is frequently used to reduce the bias of an estimator.

Note that bootstrap differs from jackknife in two ways:

Bootstrap repeatedly draws samples with full replacement.
The researcher has to decide how many repetitions are appropriate.

7. Sampling-Related Biases

There are many issues in sampling. Here we discuss four main issues.

7.1 Data-Snooping Bias

Data-snooping is the practice of analyzing the same data again and again, till a pattern that works is identified.

There are two signs that can warn analysts about the potential existence of data snooping:

Too much digging/too little confidence: Many different variables were tested, until significant ones were found. Unfortunately, many researchers do not disclose the number of variables examined in developing a model.
No story/no future: Without a reasonable economic rationale or story for why a variable should work, the variable is unlikely to have predictive power.

The best way to avoid this bias is to test the pattern on out-of-sample data to check if it holds.

7.2 Sample Selection Bias

When data availability leads to certain assets being excluded from the analysis, the resulting problem is known as sample selection bias.

Two types of sample selection biases are:

Survivorship bias: For example, many mutual fund databases provide historical information about only those funds that currently exist. Since mutual funds usually shut down after a period of poor performance, this may inflate the average performance numbers of the database.
Backfill bias: For example, if a new hedge fund is added to a given index, the fund’s past performance is also backfilled into the index. Since new funds are usually added after a period of good performance, this may inflate the index performance.

7.3 Look-Ahead Bias

A test design is subject to look-ahead bias if it uses information that was not available to market participants at the time the market participants act in the model. For example, an analyst wants to use the company’s book value per share to construct the P/B variable for that particular company. Although the market price of a stock is available for all market participants at the same point in time, fiscal year-end book equity per share might not become publicly available until sometime in the following quarter.

One way to avoid this bias is to use point-in-time (PIT) data. PIT data is stamped with the date when it was released. In the above example, PIT data of P/B would be stamped with the company’s filing or press release date rather than the fiscal quarter end date.

7.4 Time-Period Bias

A test design is subject to time-period bias if it is based on a time period that may make the results time-period specific. A short time series is likely to give period-specific results that may not reflect a longer period. If a time series is too long, fundamental structural changes may have occurred in that time period.