IFT Notes for Level I CFA^® Program

LM01 Time Value of Money

Part 3

7. Present Value of a Single Cash Flow

Let’s say that one year from today you will receive a cash flow of $110. What is the value of that $110 today? (Assume that the interest rate is 10%)

$PV=\frac{{FV}_1}{{\left(1+0.1\right)}^1}=\frac{\$110}{{\left(1+0.1\right)}^1}=\$100$

The $110 one year from today has a present value of $100. In other words, you will be indifferent between $100 today and $110 one year from today.

What if you were going to receive $121 at the end of two years, what is its present value?

$PV=\frac{{FV}_2}{{\left(1+0.1\right)}^2}=\frac{\$121}{{\left(1+0.1\right)}^2}=\$100$

Using these two examples we can write a general formula for computing PV. Given a cash flow that is to be received in N periods and an interest rate of r per period, the PV can be computed as:

$PV=\frac{{FV}_N}{{\left(1+r\right)}^N}$

where:
N = number of periods

r = rate of interest

FV = future value of investment

Instructor’s Note

Notice that this formula can also be obtained by simply rearranging the formula for FV that we studied earlier.

$FV_N=\ PV\ {\left(1\ +\ r\right)}^N \Longrightarrow PV=\frac{{FV}_N}{{\left(1+r\right)}^N}$

Based on this formula we can make two observations

For a given discount rate, the farther in the future the amount to be received, the smaller the amount’s present value.

Mathematical explanation: In the first case the PV is $110/1.1, whereas in the second case PV is $110/1.1². Since we are dividing by a larger number the PV will be lower in the second case.
Intuitive explanation: Clearly receiving a certain amount of money sooner is better than receiving the same amount of money latter.

Holding time constant, the larger the discount rate, the smaller the present value of a future amount.

In the first case PV is $110/1.1, whereas in the second case PV is $110/1.2. Clearly the PV is going to be lower in the second case, because we are dividing by a larger number.

Example

Liam purchases a contract from an insurance company. The contract promises to pay $600,000 after 8 years with a 5% return. What amount of money should Liam most likely invest? Solve using the formula and TVM functions on the calculator.

Solution:
Formula Method

$PV=\frac{{FV}_N}{{\left(1+r\right)}^N}=\frac{\$600,000}{{\left(1.05\right)}^8}=\$406,104$

Calculator Method

N = 8, I/Y = 5%, PMT = 0, FV = $600,000; CPT PV $\Longrightarrow$ PV = – $406,104

Example

Mathews wishes to fund his son, Nathan’s, college tuition fee. He purchases a security that will pay $1,000,000 in 12 years. Nathan’s college begins 3 years from now. Given that the discount rate is 7.5%, what is the security’s value at the time of Nathan’s admission?

Solution:

${PV}_3=\frac{\$1,000,000}{{\left(1.075\right)}^9}=\$521,583.47$

Example

Orlando is a manager at an Australian pension fund. 5 years from today he wants a lump sum amount of AUD40, 000. Given that the current interest rate is 4% a year, compounded monthly, how much should Orlando invest today?

Solution:

We have monthly compounding, therefore the inputs to our calculator will be

N = 5 x 12 = 60

I = 4 /12%

PMT = 0

FV = $40,000

CPT PV = – $32,760.12

8 . Non-Annual Compounding (Present Value)

When our compounding frequency is not annual, we use the following formula to compute present value:

$PV= {FV}_N (1 + \frac{r_s}{(m)})^{-mN}$

where:

r_s = the stated annual interest rate in decimal format

m = the number of compounding periods per year

N = the number of years

Let’s understand this concept using an example.

You want to know how much to deposit today to receive a lump-sum payment of $100,000 after 5 years. This amount will be invested in a 5-year certificate of deposit that offers a stated annual interest rate of 10% compounded quarterly. How much should you invest today?

Solution:

There are two methods to solve this question.

Formula Method:

FV is $100,000.

The number of compounding periods per year is 4.

The stated annual rate is 10%. So, the interest rate per period is 10%/4 = 2.5%

The total number of periods is 4 x 5 = 20.

Therefore, the present value today is:

PV=$100,000 (1+0.025)^(-20)=$61,027.09

Calculator Method:

You can also solve this problem using a financial calculator; the key strokes are given below:

N = 20, I/Y = 2.5%, FV = $100,000, PMT = 0, CPT PV = -$61,027.09

PMT is 0 because there are no intermediate payments in this example.

9. Present Value of a Series of Equal and Unequal Cash Flows

9.1. The Present Value of a Series of Equal Cash Flows

Ordinary Annuity

An ordinary annuity is a series of equal payments at equal intervals for a finite period of time. Examples of ordinary annuity: mortgage payments, pension income etc.

Consider an ordinary annuity with A = $10, r = 5% and N = 5.

We can compute the PV of this annuity using three methods

Brute-Force Method:

Simply take each cash flow and compute the PV. Add all values to get the PV for the annuity.

PV = $43.29.

Formula Method:

The present value can also be computed using the following formula:

$PV=A\ \left[\frac{1-\left(\frac{1}{{\left(1+r\right)}^N}\right)}{r}\right]$

where:

A = annuity amount

r = interest rate per period corresponding to the frequency of annuity payments

N = number of annuity payments

The term in square brackets is called the present value annuity factor (PVAF). Hence the equation above can also be written as: PV = A x PVAF.

Therefore, using the formula we get,

$PV=10\ \left[\frac{1-\left(\frac{1}{{\left(1+0.05\right)}^5}\right)}{0.05}\right]=\$43.29$

Calculator Method:

The keystrokes to solve this using a financial calculator are given below:

Keystrokes	Explanation	Display
[2nd] [QUIT]	Return to standard calc mode	0
[2^nd] [CLR TVM]	Clears TVM Worksheet	0
5 [N]	Five years/periods	N = 5
5 [I/Y]	Set interest rate	I/Y = 5
0 [FV]	Set to 0 because there is no final payment other than the periodic annuity amounts	FV = 0
10 [PMT]	Set annuity payment	PMT = 10
[CPT] [PV]	Compute present value	PV = -43.29

Annuity Due

With an annuity due the first payment is received at the start of the first period. So if we have an annuity due with A = $10, r = 5% and N = 5. The cash flows will be

Again, there are three methods to calculate the PV of this annuity due.

Brute-Force method

Take each cash flow and compute the PV. Add all values to get the PV for the annuity.

PV = $45.46.

Notice that with an annuity due you are receiving money faster, which means that the

PV _{annuity due} ($45.46) > PV _{ordinary annuity} ($43.29).

Formula method:

We can also use the following formula:

$PV=A\left[\frac{1-\frac{1}{{\left(1+r\right)}^N}}{r}\right](1+r)$

where:

A = annuity amount

r = interest rate per period corresponding to the frequency of annuity payments

N = number of annuity payments

Therefore using the formula,

$PV=10\left[\frac{1-\frac{1}{{\left(1+0.05\right)}^5}}{0.05}\right]\left(1+0.05\right)=\$45.46$

Instructor’s Note:
Notice that $A\left[\frac{1-\frac{1}{{\left(1+r\right)}^N}}{r}\right]$ is basically the formula for computing the PV of an ordinary annuity. If you use the ordinary annuity formula the PV that you get will be at time period -1. So this needs to be taken forward one period by multiplying it by (1 + r)

Calculator Method:

Set the calculator to BGN mode. This tells the calculator that payments happen at the start of every period. (The default calculator setting is END mode which means that payments happen at the end of every period). The keystrokes are shown below:

Keystrokes	Explanation	Display
[2nd] [BGN] [2nd] [SET]	Set payments to be received at beginning rather than end	BGN
[2nd] [QUIT]	Return to standard calc mode	BGN 0
[2nd] [CLR TVM]	Clears TVM Worksheet	BGN 0
5 [N]	Four years/periods	BGN N = 5
5 [I/Y]	Set interest rate	BGN I/Y = 5
10 [PMT]	Set payment	BGN PMT = 10
0 [FV]	Set future value	BGN FV = 0
[CPT] [PV]	Compute present value	BGN PV = -45.46
[2nd] [BGN] [2nd] [SET]	Set payments to be received at the end	END
[2nd] [QUIT]	Return to standard calc mode	0

Always remember to put your calculator back in the END mode after you are done with the calculations.

9.2.The Present Value of a Series of Unequal Cash Flows

When we have unequal cash flows, we can first find the present value of each individual cash flow and then sum the respective present values.

Let’s say that we have the following cash flows:

Time period	Cash Flow
1	$100
2	$200
3	$300

Assuming a discount rate of 10%, the PV of these cash flows can be computed as:

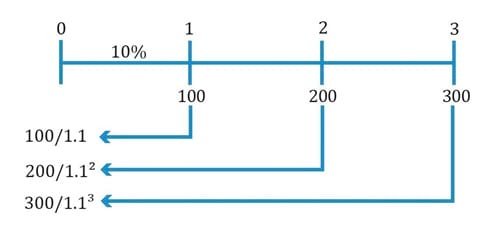
PV = 100/1.1 + 200/1.1² + 300/ 1.1³ = $481.59

Example

Andy makes an investment with the expected cash flow shown in the table below. Assuming a discount rate of 9% what is the present value of this investment?

Time Period	Cash Flow($)
1	50
2	100
3	150
4	200
5	250

Solution:

PV = 50/1.09 + 100/1.09² + 150/1.09³ + 200/1.09⁴ + 250/1.09⁵ = $550.03

We can also use the cash flow register on our financial calculator to solve this problem quickly. The key strokes are as follows:

Keystrokes	Explanation	Display
[2nd] [QUIT]	Return to standard mode	0
[CF] [2nd] [CLR WRK]	Clear CF Register	CF = 0
0 [ENTER]	No cash flow at t = 0	CF0 = 0
[↓] 50 [ENTER]	Enter CF at t = 1	C01 = 50
[↓] [↓] 100 [ENTER]	Enter CF at t = 2	C02 = 100
[↓] [↓] 150 [ENTER]	Enter CF at t = 3	C03 = 150
[↓] [↓] 200 [ENTER]	Enter CF at t = 4	C04 = 200
[↓] [↓] 250 [ENTER]	Enter CF at t = 5	C05 = 250
[↓] [NPV] [9] [ENTER]	Enter discount rate	I = 9
[↓] [CPT]	Compute NPV	550.03

10. Present Value of a Perpetuity

A perpetuity is a series of never ending equal cash flows. The present value of perpetuity can be calculated by using the following formula:

$PV=\frac{A}{r}$

where:

A = annuity amount

r = discount rate

Let’s say that we have a really simple perpetuity where we receive $10 at the end of every year forever, and let’s say that the interest rate is 5%.

The PV of this perpetuity can be computed as:

$PV=\frac{10}{0.05}=\$200$

Instructor’s Note:
Keep in mind that the present value of $200 is one period before the first cash flow. Many students show the present value of $200 at the same time as the first cash flow, which is incorrect.

10.1. Present Values Indexed at Times Other Than t=0

An annuity or perpetuity beginning sometime in the future can be expressed in present value terms one period prior to the first payment. That value can then be discounted back to today’s present value.

Let’s say you are offered a cash flow of $10 at the end of year 5, end of year 6, and so on forever. What is the PV of these cash flows, assuming a discount rate of 10%?

The PV of the perpetuity at the end of year 4 can be computed as:

${PV}_4=\frac{10}{0.1}=\$1,00$

This value has to be discounted back four periods to get the PV at time period 0.

PV₀ = $100/1.1⁴ = $68.30

Example

Bill Graham is willing to pay for a perpetual preferred stock that pays dividends worth $100 per year indefinitely. The first payment will be received at t = 4. Given that the required rate of return is 10%, how much should Mr. Graham pay today?

Solution:

The time line for this scenario is