101 Concepts for the Level I Exam

Essential Concept 92: Factor Models in Return Attribution

Active managers try to generate a return above a given benchmark by holding securities in weights different than the benchmark. The active return on a portfolio is the return on a portfolio minus the benchmark’s return.

$\mathrm{Active\ return\ =\ }{\mathrm{R}}_{\mathrm{P}}\mathrm{-}{\mathrm{R}}_{\mathrm{B}}$

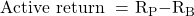
Multifactor models help us understand the sources of a manager’s return relative to a benchmark. Analysts favor fundamental multifactor models to decompose the sources of returns as they are easier to explain compared to statistical models.

Using a factor model, we can decompose a portfolio manager’s active return as the sum of two components:

Return from factor tilts: product of the portfolio manager’s factor tilts (overweight or underweight relative to the benchmark factor sensitivities) and the factor returns. For example, if a benchmark’s sensitivity to market risk is 1.0 and an active portfolio’s sensitivity to market risk 1.2, the market risk factor tilt here is 1.2 – 1.0 = 0.2.
Return from asset selection: part of active return reflecting the manager’s skill in individual asset selection. That is, overweighting securities that outperform the benchmark or underweighting securities that underperform the benchmark.

The following equation shows the decomposition of active return into these two components:

$\noindent Active\ return = $\sum\limits_{j=1}^{K}{\left[{\left(\mathrm{Portfolio\ sensitivity}\right)}_{\mathrm{j}}\mathrm{-}{\left(\mathrm{Benchmark\ sensitivity}\right)}_{\mathrm{j}}\right]\mathrm{*}{\left(\mathrm{Factor\ return}\right)}_{\mathrm{j}}\mathrm{+Asset\ selection}}$$