101 Concepts for the Level I Exam

Essential Concept 2: Standard Error of Estimate, Coefficient of Determination, Confidence Interval for a Regression Coefficient

Standard error of estimate (SEE) measures how well a given linear regression model captures the relationship between the dependent and the independent variables.

$\mathrm{SEE=}{\left(\sum^{\mathrm{N}}_{\mathrm{i\ =\ 1}}{\frac{{\left({\mathrm{Y}}_{\mathrm{i}}\mathrm{\ -\ }\widehat{{\mathrm{b}}_0}\mathrm{\ -\ }\widehat{{\mathrm{b}}_{\mathrm{1}}}{\mathrm{X}}_{\mathrm{i}}\right)}^{\mathrm{2}}}{\mathrm{n-2}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{=}{\left(\frac{\sum^{\mathrm{N}}_{\mathrm{i\ =\ 1}}{{\widehat{\left({\mathrm{\epsilon }}_{\mathrm{i}}\right)}}^{\mathrm{2}}}}{\mathrm{n-2}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{\ =}{\left(\frac{\mathrm{SSE}}{\mathrm{n-2}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}$

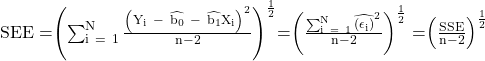The lower the SEE, the better the fit of the regression line. Also, note that the sum of the squared error terms can be written as SSE.

Coefficient of determination (R²) measures the fraction of the total variation in the dependent variable that is explained by the independent variable.

Total variation = Unexplained variation + Explained variation

${\mathrm{R}}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{Explained\ variation}}{\mathrm{Total\ variation}}$

In a regression with one independent variable, R²is the square of the correlation between the dependent and independent variables. The higher the R², the more useful the model. has a value between 0 and 1.

The confidence interval for a regression coefficient is given by:

$\mathrm{Confidence\ interval=}\widehat{{\mathrm{b}}_{\mathrm{1}}}\mathrm{\pm }{\mathrm{t}}_{\mathrm{c}}{\mathrm{s}}_{\widehat{{\mathrm{b}}_{\mathrm{1}}}}$