101 Concepts for the Level I Exam

Essential Concept 80: The BSM Model

The inputs to the BSM model are:

Price of underlying stock, S
Continuously compounded risk-free rate, r
Time to maturity in years, T
Strike price, X
Volatility of the underlying in annual percentage terms, σ

The BSM model for non-dividend paying stock is:

c = SN(d₁) – e^–rTXN(d₂)

p = e^–rTXN(–d₂) – SN(–d₁)

where:

$\mathrm{d}}_{\mathrm{1}}\mathrm{=}\frac{\mathrm{ln}\mathrm{}\mathrm{(S/X)+(r+}{\mathrm{\sigma }}^{\mathrm{2}}\mathrm{/2)T}}{\mathrm{\sigma }\sqrt{\mathrm{T}}}$

$d${}_{2}$ = d${}_{1}$ $\mathrm{-}$ $\sigma$$\sqrt{\mathrm{T}}$

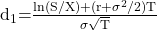
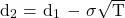
Using the above inputs, the BSM model can be used to predict:

Call option price, c
Put option price, p

Instructor’s Note:

The following tips will help you remember the formulas.

c = SN(d₁) – e^–rTXN(d₂)

p = e^–rTXN(–d₂) – SN(–d₁)

A call option is of the form S- X, whereas a put option is of the form X – S.
The present value of strike price X is obtained by multiplying it by e^–rT
d₁is associated with S, whereas d₂is associated with X
For call options we use positive values of d₁ and d₂. Whereas, for put options we use negative values of d₁ and d₂.